As energias cinéticas translacionais das moléculas de um gás são distribuídas de acordo com a distribuição de energia de Maxwell-Boltzmann, Equação 17-38.

(a) Determine o valor mais provável da energia cinética translacional (em termos de temperatura ) e compare esse valor com o valor médio.

(b) Esboce um gráfico da distribuição de energia cinética translacional e identifique a energia mais provável e a energia média. (Não se preocupe em calibrar a escala vertical do gráfico.)

(c) Seu professor diz: ″ Basta olhar para o gráfico para ver que a energia cinética translacional média é consideravelmente maior que a mais provável energia cinética translacional. ″ Quais características do gráfico sustentam sua afirmação?

Agora a gente deriva e iguala a 0 para achar os picos:

Resolvendo para :

Portanto, a energia média das moleculas é dada por:

Fazendo uma relação:

b) O gráfico a seguir da distribuição de energia foi plotado usando um programa de planilha. Observe que foi definido como e que, conforme previsto em nosso resultado em (a), o valor de pico ocorre para .

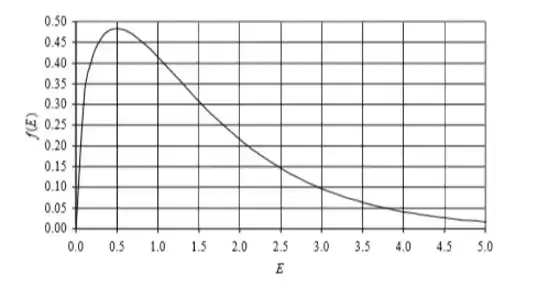
c) O gráfico aumenta de zero para o pico muito mais rapidamente do que cai à direita do pico. Como a distribuição é tão fortemente inclinada à direita do pico, as moléculas externas com energias relativamente altas puxam a média () para a direita do valor mais provável ().