Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 30.Exercícios e Problemas - Ex. 41
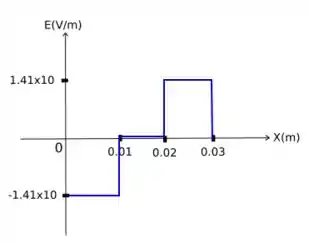
A FIGURA P30.41 mostra a vista lateral de três eletrodos metálicos carregados. Desenhe o gráfico (a) de versus e (b) de V versus x para a região .
Passo 1
Fala galera, tudo tranquilo? Fiquei de olho na figura para poderem acompanhar a resolução. Vamos lá!
Podemos visualizar esses eletrodos como capacitores de placas paralelas, perceba que temos uma placa negativa do lado esquerdo e direito. Ao centro uma placa maior positiva. Podemos separar elas em 2 capacitores de placas paralelas com cargas de , pegando metade da placa no centro para a direita e para a esquerda formando dois capacitores de placas paralelas. Assim o campo elétrico para um capacitor é dado pela equação abaixo.
O campo na região entre , flue da carga + para a carga -, apontando para o lado esquerdo. Já o campo na região aponta para a direita com a mesma intensidade do lado esquerdo.
Na região entre o campo é nulo no interior de materiais condutores.
Passo 2
Agora trabalhando com o potencial eletrostático temos a seguinte equação
, onde X varia nos pontos onde se encontram os capacitores. Ou seja:
, e
, assumindo a posição da placa negativa do lado esquerdo no ponto x = 0, o potencial é dado apenas pelo ponto x = 0.01m=1cm, deste modo:
crescente no intervalo de 0cm a 1cm
Se , sendo o , significa dizer que . Então no ponto 1cm a 2cm o potencial é constante.
Para o intervalo de 2cm a 3cm o potencial é idêntico ao intervalo de 0cm a 1cm mas, decrescente.
Resposta
