Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 34.Exercícios e Problemas - Ex. 40

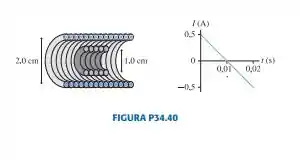
A FIGURA P34.40 mostra uma bobina com 1,0   c m de diâmetro, 5 espiras e resistência R =   0,10   Ω , dentro de um solenoide de 2,0   c m de diâmetro e 8,0   c m de comprimento, com 120 espiras e que conduz a corrente representada no gráfico. A corrente é positiva no sentido horário, quando vista da esquerda. Determine a corrente na bobina em   t =   0,010   s .

Passo 1

Faaaaaala, galera... Tranquileba??

Sabemos que:

ε = d ϕ b d t

E para uma bonina:

ε = N b o b i n a d ϕ b d t  

E:

ϕ b = ∮ S B → ∙ n v e r s o r d A →

Sendo B constante:

ϕ b = B * A

E sabemos que o campo elétrico em um solenoide é:

B = μ 0 N I l

Assim:

ϕ b = μ 0 N I l π r 2

Bora pro próximo item?!

Passo 2

De modo que:

ε = d d t μ 0 N I   N b o b i n a l π r 2 = μ 0 N l π r 2   N b o b i n a   d I d t

E pede-se a corrente na espira, logo:

I e s p i r a = 1 R   ε

I e s p i r a   = 1 R μ 0 N l π r 2   N b o b i n a   d I d t

Temos tudo, e o valor de corrente no tempo obteremos através do gráfico.

Passo 3

Temos que 0 ≤ t ≤ 0.01   s :

d I d t = 0 - 05 A 0.01 - 0 s = 50   A s

Assim:

I e s p i r a   = 1 R μ 0 N l π r 2   N b o b i n a d I d t

Aplicando números:

I e s p i r a   = 1 ( 0.10   Ω ) 4 π × 10 - 7   T m A ( 5 ) ( 120 ) l π 1 2 1 × 10 - 2 m 2   50 A s

Concluímos que:

I e s p i r a     p e q u e n a = 0.37   m A

Resposta

I e s p i r a     p e q u e n a = 0.37   m A

Ver Outros Exercícios desse livro