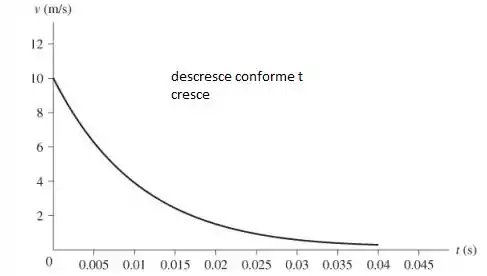
Vamos examinar os detalhes da frenagem por correntes de Foucault. Uma espira quadrada com lados de comprimento l é atirada, com velocidade , para dentro de uma região onde existe campo magnético uniforme B. O campo é perpendicular ao plano da espira. A espira tem massa m, resistência R e entra no campo em s. Suponha que a espira esteja se movendo para a direita, ao longo do eixo x, e que o campo começa a existir em .
- Obtenha uma expressão para a velocidade da espira em função do tempo enquanto ela adentra o campo magnético. Despreze efeito da gravidade e suponha que a borda traseira da espira ainda não entrou na região do campo.
- Calcule e desenhe um gráfico de v correspondente ao intervalo para o caso em que e. A borda traseira da espira não atinge o campo durante esse intervalo de tempo.
Passo 1
Faaaaaala, galera... Tranquileba??
Sabemos por definição que:
E que:
Sendo
Assim:
Considerando que o campo eletrico é constante:
Bora pro próximo passo?!
Passo 2
E então, a corrente é:
Fazendo um esboço da situação dada, temos:
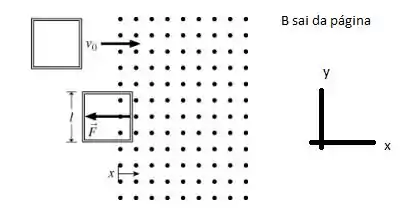
Vemos que , assim:
Mas
Assim:
E com ess corrente podemos achar a força magnética do fio da espira:
E pela segunda lei de newton:
Assim:
Integrando de ambos os lados com limites de e , temos:
Onde
Passo 3
Para b)
Aplicando os valores na equação achada anteriormente:
Concluímos que:
Assim:
Gerando um gráfico deste modo:
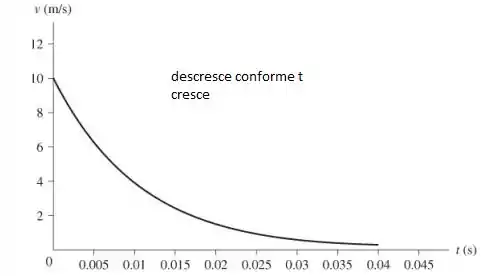
Resposta
Para a)
Onde
Para b)