Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Termodinâmica Óptica- Ed: 2º - Capítulo 19.Exercícios e Problemas - Ex. 72

A FIGURA PD19.n representa o ciclo Diesel. Ele é semelhante ao ciclo Otto (ver Problema PD19.71). entretanto há duas diferenças importantes. Primeiro, o combustível não é admitido até que o ar seja . completamente comprimido. no ponto 2. Devido à alta temperatura oo término de uma compressão adiabática, o combustível começa a queimar espontaneamente. (Não existem velas de ignição cm um motor a diesel!) Segundo, a combustão ocorre mais lentamente, enquanto o combustíve l continua sendo injetado. Isso torna o estágio da ignição um processo a pressão constante. O ciclo mostrado, para um cilin~ro de motor a diesel, possibilita a expansão V.,,., - V m•• de 1000 cm' e tem uma razão de compressão r = V ,,,./V""" = 21. Estes são valores típicos para um caminhão a diesel. O mOlor opera com entrada de ar ( y = 1.40) a 25ºC e pressão de 1,0 atm. A quantidade de combusúvel io jetada no ci 1 i ndro tem calor de combustão de l 000 J. a. De1ennine p. V e T nos quatro vértices do ciclo. Apresente seus resultados em uma rabeia. b. Qual é o trabalho resultante rea lizado pelo cilindro durante um ciclo completo? c. Qual é o rendimento térmico deste motor? d. Qual é a potência de saída. em kW e cm hp (1 hp = 746 W), de um motor a diesel de oito cilindros que funciona a 2400 rpm?

Passo 1

E aiii gente, tudo bom com vocês?

Então vamos resolver essa questão bem legal aqui e passo a passo pra gente tirar 10 na provinha!

Vamo lá!

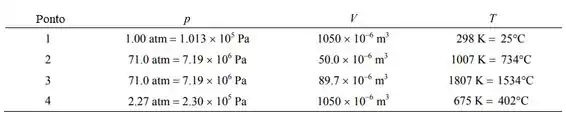
Letra a:

Será útil fazer alguns cálculos usando a taxa de compressão, que é:

r = V m a x V m i n = V 1 V 2 = 1050 c m 3 50 c m 3 = 21

O número de mols de gás é:

n = p 1 V 1 R T 1 = 1.013 × 10 5 P a 1050 × 10 - 6 m 3 8.31 J m o l K 25 + 273 K = 0.0430 m o l

Para um processo adiabático,

p 1 V 1 γ = p 2 V 2 γ ⇒ p 2 = V 1 V 2 γ p 1 = r γ p 1 = 21 1.40 × 1 a t m = 71.0 a t m = 7.19 × 10 6 P a

T 1 V 1 γ - 1 = T 2 V 2 γ - 1 ⇒ T 2 = V 1 V 2 γ - 1 T 1 = r γ - 1 T 1 = 21 0.41 × 298 K = 1007 K

O processo 2   →   3 é um aquecimento isobárico com Q   =   1000   J . O aquecimento de pressão constante obedece:

Q = n C p Δ T ⇒ Δ T = Q n C p

Passo 2

O gás tem uma taxa de calor específica γ = 1.40 = 7 / 5 ,   ent ã o   C V = 5 2 R   e   C P = 7 2 R . Conhecendo o C p , podemos calcular primeiro Δ T = 800 K e então T 3 = T 2 + Δ T = 1807 K . Finalmente, para um processo isobárico, temos,

V 2 T 2 = V 3 T 3 ⇒ V 3 = T 3 T 2 V 2 = 1807 K 1007 K 50 × 10 - 6 m 3 = 89.7 × 10 - 6 m 3

O processo 3   →   4 é uma expansão adiabática para V 4 = V 1 . Por isso,

p 3 V 3 γ = p 4 V 4 γ ⇒ p 4 = V 3 V 4 γ p 3 = 89.7 × 10 - 6 m 3 1050 × 10 - 6 m 3 1.4 7.19 × 10 6 P a = 2.30 × 10 5 P a = 2.27 a t m

T 3 V 3 γ - 1 = T 4 V 4 γ - 1 ⇒ T 4 = V 3 V 4 γ - 1 T 3 = 89.7 × 10 - 6 m 3 1050 × 10 - 6 m 3 0.4 1807 K = 675 K

Passo 3

Letra b:

Para o processo adiabático 1   →   2 ,

W s 12 = p 2 V 2 - p 1 V 1 1 - γ = - 633 J

Para o processo isobárico 2   →   3 ,

W s 23 = p 2 Δ V = p 2 V 3 - V 2 = 285 J

Para o processo adiabático 3   →   4 ,

W s 34 = p 4 V 4 - p 3 V 3 1 - γ = 1009 J

Para o processo isocórico 4 → 1 , W s 41 = 0 J . Então:

W s c i c l o = W sa í da   = W s 12 + W s 23 + W s 34 + W s 41 = 661 J

Passo 4

Letra c:

A eficiência é:

η = W sa í da   Q H = 661 J 1000 J = 66.1 % ≈ 66 %

Passo 5

Letra d:

A potência de saída de um cilindro é:

661 J   ciclo   × 2400 c i c l o s m i n × 1 m i n 60 s e g = 26,440 J s = 26.4 k W

Para um motor de 8 cilindros, a potência será de 211   k W ou 283   H P .

Resposta

  1. Ver resposta
  2. 661J
  3. 66%
  4. 26.4W
Ver Outros Exercícios desse livro