Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 34.Exercícios e Problemas - Ex. 53

Um fio de comprimento l, massa m e resistência R desliza sobre um longo trilho metálico em forma de U e inclinado para cima em um ângulo θ . O trilho é livre de atrito e possui resistência elétrica nula. Um campo magnético vertical B preenche a espira formada pelo trilho e pelo fio deslizante.

  1. Obtenha uma expressão para a corrente induzida I quando o fio deslizante se move a uma velocidade v.
  2. Mostre que o fio deslizante atinge uma velocidade terminal v t e r m e encontre uma expressão para ela.

Passo 1

Faaaaaala, galera... Tranquileba??

Fazendo um desenho que ilustra a situação dada no enunciado, temos:

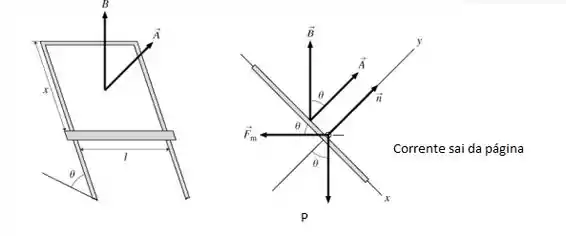
Bora pro próximo passo?!

Passo 2

Para a)

Sabemos que:

ε = d ϕ d t

E que:

ϕ = ∫ B * d A  

Sendo B constante:

ϕ = * B * A * cos ⁡ θ

Assim:

ε = d d t ( B A cos ⁡ θ )

Sabemos por definição que:

I = ε R

Logo:

I = 1 R   d d t ( B A c o s   θ )

Veja que A = l x , considerando que B seja constate:

I = 1 R   l B cos ⁡ θ d d t ( x )

I = l B v R cos ⁡ θ

Passo 3

Para b)

Sabemos que a força que um fio com corrente produz É:

F f i o = I l B

Assm:

F f i o = l B v R cos ⁡ θ l B = B 2 l 2 v cos ⁡ θ R

Usando o diagrama de corpo livre dado no passo a):

∑ F x = - F i o cos ⁡ θ + P sin ⁡ θ = m a x

A velocidade terminal é atingida quando a aceleração é nula, logo:

F f i o cos ⁡ θ = P   s i n   θ

B 2 l 2 v cos ⁡ θ R cos ⁡ θ = m g sin ⁡ θ

v = R m g sin ⁡ θ B 2 l 2 cos 2 ⁡ θ = R m g tan ⁡ θ B 2 l 2 cos ⁡ θ

Resposta

Para a)

I = l B v R cos ⁡ θ

Para b)

v = R m g tan ⁡ θ B 2 l 2 cos ⁡ θ

Ver Outros Exercícios desse livro