Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 2.Problemas - Ex. 9
Uma partícula de massa e carga está vinculada a morver-se sobre a mediatriz do segmento que liga duas cargas positivas , separadas por uma distância . Inicialmente, a partícula está a uma distância do centro desse segmento. Mostre que ela executa um movimento harmônico simples em torno do centro, e calcule a frequência angular de oscilação.
Passo 1
Vamos resolver essa parada!
Primeiro podemos verificar as forças que agem sobre a carga . Veja a figura.
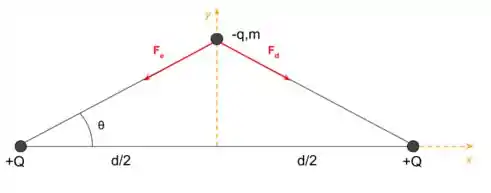
Se liga, como a carga do lado esquerdo é igual a do lado direito e as distâncias delas em relação a carga são iguais, podemos dizer que o módulo da força elétrica exercido por ambas são iguais.
Passo 2
Analisando as forças na direção temos que
Fazendo o somatório das forças na direção temos
De boa, né?!Agora vamos fazer a mesma coisa para as forças na direção .
Fazendo as somas temos
Passo 3
O podemos calcular através da fórmula da força elétrica
Sabendo que
Podemos reescrever
Passo 4
Agora vamos relacionar a força com a equação do movimento, para verificar que ela executa um MHS
No enunciado foi pedido para considerarmos que . Sendo assim, para facilitar nossas contas, vamos trocar por .
Agora faremos uma expansão em série em torno de , temos
Pronto, só precisamos substituir na equação
Passo 5
Como a forma da equação no MHS é
Comparando com a expressão que encontramos, temos