Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Problemas - Ex. 61
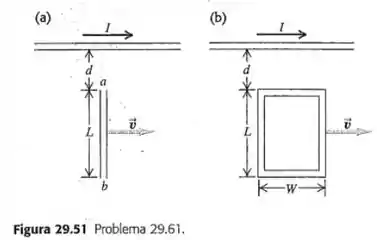
O fio retilíneo longo indicado na figura 29.51a conduz uma corrente constante . Uma barra metálica de comprimento se move com velocidade constante , como indica a figura. O ponto está a uma distância do fio.
Calcule a fem induzida na barra.
Qual dos dois pontos, ou , possui potencial mais elevado?
Se a barra for substituída por uma espira retangular de resistência (Figura 29.51a), qual será o módulo da corrente induzida na espira?
Passo 1
Temos que o campo magnético para o fio é dado por
E varia ao longo do comprimento da barra. Em todos os pontos da barra, tem direção entrando na página. Dessa forma vamos dividir a barra em fatias finas. Assim, a fem induzida em cada fatia será dada por
Onde é direcionado para o fio, então,
Portanto, a fem total induzida na barra será dada por
Passo 2
Agora, para calcularmos o último item e terminarmos o nosso problema vamos utilizar a lei de Faraday para encontrar a corrente induzida. Temos que a medida que o loop de move para a direita, o fluxo magnético através dele não muda, então, temos
Resposta
tem um potencial maior do que