Um fio muito longo e cilíndrico, de raio , transporta uma corrente uniformemente distribuída através da seção reta do fio. Calcule o fluxo magnético através de um retângulo que possui um lado com comprimento descendo pelo centro do fio e outro lado de comprimento , como indica a figura 29.49 (veja o problema 29.7).
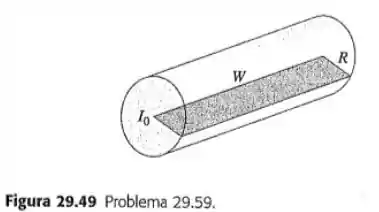
Passo 1
Para essa questão procederemos da seguinte forma: encontraremos o campo magnético a uma distância do centro do fio. Dividiremos o retângulo em faixas estreitas de largura , para assim encontrarmos o fluxo através de cada faixa e integrar para encontrar o fluxo total. Sendo assim, como é mostrado no exemplo resolvido do livro podemos utilizar a lei de Ampère para mostrar que o campo magnético dentro do fio, a uma distância do eixo, é
Consideremos então uma pequena faixa de comprimento e largura , a uma distância do eixo do fio. O fluxo através da faixa é de
Sendo assim, o fluxo total através do retângulo será dado por