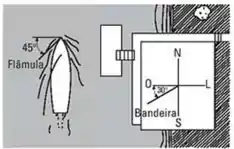
A flâmula presa na frente do mastro de um veleiro estende-se para trás, segundo um ângulo de , como ilustra a Fig. , mas a bandeira na sede do clube se estende segundo o ângulo de , para o sul, a partir da direção o oeste. (a) Se a velocidade do barco for de , qual será a velocidade do vento? (b) Calcule a velocidade aparente do vento para um observador sobre o barco.
Passo 1
E aí, beleza?? Para resolver esse problema, vamos considerar o seguinte diagrama, montado no referencial do barco. Perceba que haverá uma composição de velocidades aqui: o vento, em relação ao clube, possui uma inclinação de , enquanto que em relação ao barco, possui uma inclinação de , pois recebe a adição de um vetor de módulo igual ao da velocidade do barco, mas no sentido contrário:
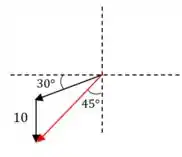
Assim, o vetor em vermelho corresponde à velocidade do vento no referencial do barco, enquanto o vetor preto inclinado de corresponde à velocidade do vento em relação ao clube.
Assim, sendo o módulo da velocidade do vento em relação ao cais e a velocidade do vento em relação ao barco, então vem:
Como , então:
Passo 2
Para
Portanto: