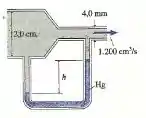
O ar flui através do tubo da figura abaixo com uma vazão de . Suponha que o ar seja um fluido ideal. Qual é a altura h de mercúrio no ramo direito do tubo em U
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!!
Aqui, vamos ser mais diretos em usar a lei de Bernoulli, que é dada pela seguinte equação
Entendemos que a variação de é dada por
Que por sua vez, é igual a
Agora, vamos considerar uma coisa, vamos isolar as velocidades em duas partes, baseando-se na taxa de fluxo, com isso, temos que:
Daqui, temos duas coisas
Lembrando que a gente pode usar qualquer parte da igualdade, afinal, ela é uma igualdade. Agora, desde que a área seja dada por , nós temos que
E consequentemente, temos que:
Passo 2
Já temos tudo encaminhado já, agora, é só trabalhar com a diferença de pressão, como já temos as relações das velocidades, logo
Podemos igualar as duas expressões para a diferença de pressão e encontrar a altura, como segue
Isolando o , obtemos o seguinte resultado
Agora, é só substituir os valores numéricos para encontrar a altura