Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 60
Uma força horizontal de empurra um bloco de para cima, em um plano inclinado sem atrito que forma um ângulo de com a horizontal. (a) Qual é a força normal que o plano inclinado exerce sobre o bloco? (b) Qual é a magnitude da aceleração do bloco?
Passo 1
a) Oi pessoal, tudo bem? A gente tem um bloco sendo empurrado através um plano inclinado por uma força horizontal .
Esse plano faz com a horizontal. O primeiro a se fazer nessas questões que envolvem forças é desenhar o diagrama de corpo livre para entender melhor a situação. O nosso fica assim:
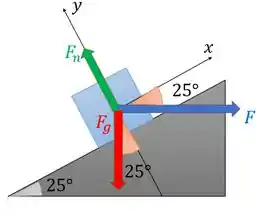
Temos a força em azul. Como o bloco tem massa , ele vai estar sob ação da gravidade, ou seja, há a força peso puxando o bloco para baixo.
E como há contato entre o bloco e a superfície, a gente precisa considerar a força normal que a superfície aplica perpendicularmente ao bloco. Ele fala para desconsiderarmos o atrito, então com esse diagrama a gente já representou todas as nossas forças.
Ele pede a magnitude de . Como essa força está perpendicular ao plano inclinado, vai ser mais vantagem usar um sistema de referência que coloque um dos eixos coincidindo com essa força, beleza?
Como a gente tem forças atuando e um bloco em movimento, a gente pode pensar em usar a segunda lei de Newton:
para gente achar o que ele pede. Bora lá!
Passo 2
Como está na nossa direção , vamos aplicar a segunda lei de Newton nessa direção para achar .
Ela fica assim:
O bloco está se movendo apenas na direção , então a aceleração dele em é nula . E esse é a soma das componentes de todas as forças em . Nossa expressão então fica:
Onde , já que o ângulo que orienta é oposto a , e ela está no sentido negativo de . porque está no eixo . porque o ângulo que orienta está colado em , e a força aponta para baixo. Substituindo, ficamos com:
Lembrando que a força peso é dada por :
Substituindo os valores, temos:
Passo 3
b) Para saber a magnitude da aceleração do bloco, devemos usar a segunda lei de Newton no eixo onde há movimento, ou seja, no eixo x:
A gente tem que é a soma de todas as componentes da forças em . está em , então ela não aparece nessa soma. Temos , porque aponta para o sentido negativo de e seu ângulo está oposto a .
E temos que , já que o ângulo que orienta está colado em . Somando essas componentes e substituindo em :
Lembrando que :
Substituindo os valores, temos: