Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 64
Um bloco de 10 kg está suspenso do teto de um elevador por uma corda feita para aguentar uma tensão de 150 N. Pouco depois do elevador começar a subir, a corda se rompe. Qual foi a mínima aceleração do elevador quando a corda se rompeu?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Ele quer a aceleração mínima do elevador para arrebentar a cordinha que prende o bloco, quando esse elevador começa a subir. Ou seja, esse elevador vai passar a ter uma aceleração para cima que o tira do repouso e coloca sua velocidade no sentido para cima.
Quando a gente pensa em problemas de elevador, é sempre importante associar que a aceleração do elevador e de um objeto em repouso dentro dele serão iguais. Então para achar essa aceleração que ele pede, podemos achar a aceleração do bloco!
E dentro disso, lembrar da segunda lei de Newton:
E o que essa equaçãozinha fofa nos diz? Dentre muitas coisas, ela diz que o sentido da aceleração do objeto é o mesmo da força resultante sobre ele.
Depois de pensar nessas coisinhas, vamos botar a mão na massa e descobrir do bloco suficiente para arrebentar a cordinha. Ou seja, que faz a tensão na corda chegar ao limite de . Bora!
Passo 2
Depois de entender como funciona essa relação do elevador com o objeto, é importante a gente fazer o diagrama de corpo livre do bloco. Por que? Porque a gente vai achar a aceleração dele, que é a mesma do elevador.
O objeto está preso no teto do elevador por uma cordinha. Se tem cordinha, então tem uma força nessa cordinha que mantém o objeto preso, que chamamos tensão . E se o objeto tem massa, ele vai estar sob ação da gravidade, ou seja, há força peso puxando ele para baixo.
Mas ele está dentro do elevador. E o elevador sobe acelerando. Ou seja, há uma aceleração sobre ele apontando para cima.
Se a aceleração do elevador está para cima, a aceleração do objeto também vai estar. E vimos que pela segunda lei de Newton, se a aceleração sobre o objeto está para cima, a força resultante sobre ele também deve estar.
E se a força resultante está para cima, significa que a força que está para cima é maior do que a força que está para baixo. Ou seja, no nosso diagrama, vai aparecer menor que . Fica assim:
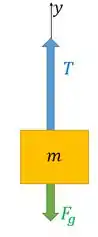
Note que a força peso é menor que a tensão na corda. Isto se dá justamente porque a força resultante está para cima.
Passo 3
Mas a gente quer saber o que faz com que a corda arrebente. Então a gente quer saber o valor de , sabendo que (a tensão limite na corda).
Para encontrar a aceleração, podemos aplicar a segunda lei de Newton para a direção , onde há aceleração. Ela fica assim:
Nessa direção temos para cima (positiva) e para baixo (negativa), então o somatório fica
Isolando quem a gente quer
Lembrando que a força peso é dada por
Substituindo os valores do enunciado, temos: