Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 40.Exercícios - Ex. 32

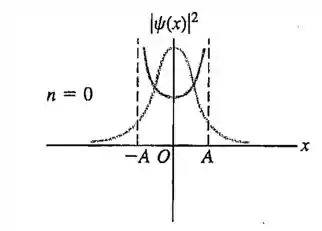
Na função de onda Ψ ( x )   do nível fundamental do oscilador harmônico dada pela equação Ψ ( x ) = C e - m k x 2 / 2 h 2 π , Ψ 2 atinge seu valor máximo em x = 0 . a)Calcule a razão entre Ψ 2 para x = + A e Ψ 2 para x = 0 , onde A é dado pela equação 1 2 k A 2 = n + 1 2 h 2 π ω com n = 0 para o nível fundamental. b)Calcule a razão entre Ψ 2 para x = + 2 A e Ψ 2 para x = 0 . Em cada caso seu resultado está de acordo com a informação indicada na figura?

Passo 1

Sabemos que a função de onda é:

Ψ ( x ) = C e - m k x 2 / 2 h 2 π

Então a norma da função de onda será:

Ψ 2 = C 2 e - m k x 2 / h 2 π

Podemos então calcular para o caso x = 0 , que será:

Ψ ( 0 ) 2 = C 2 e - m k 0 2 / h 2 π

Ψ ( 0 ) 2 = C 2

Passo 2

Podemos também encontrar o valor da amplitude usando a relação:

1 2 k A 2 = n + 1 2 h 2 π ω

para n = 0 :

1 2 k A 2 = 1 2 h 2 π ω

A 2 = h 2 π ω k

Passo 3

letra a)

A razão entre Ψ ( + A ) 2 e Ψ ( 0 ) 2 será:

Ψ ( + A ) 2 Ψ ( 0 ) 2 = C 2 e - m k A 2 / h 2 π C 2

Ψ ( + A ) 2 Ψ ( 0 ) 2 = e - m k A 2 / h 2 π

Como sabemos quem é a amplitude:

Ψ ( + A ) 2 Ψ ( 0 ) 2 = e - m k h 2 π ω k / h 2 π

Ψ ( + A ) 2 Ψ ( 0 ) 2 = e - m k ω = e - 1 ω ω

Ψ ( + A ) 2 Ψ ( 0 ) 2 = 0,368

Passo 4

letra a)

A razão entre Ψ ( + 2 A ) 2 e Ψ ( 0 ) 2 será:

Ψ ( + A ) 2 Ψ ( 0 ) 2 = C 2 e - m k 2 A 2 / h 2 π C 2

Ψ ( + A ) 2 Ψ ( 0 ) 2 = e - 4 m k A 2 / h 2 π

Como sabemos quem é a amplitude:

Ψ ( + A ) 2 Ψ ( 0 ) 2 = e - 4 m k h 2 π ω k / h 2 π

Ψ ( + A ) 2 Ψ ( 0 ) 2 = e - 4 m k ω = e - 4 1 ω ω

Ψ ( + A ) 2 Ψ ( 0 ) 2 = 1,83 ⋅ 10 - 2

Passo 5

Tanto nossos resultados quanto a figura, mostram que a probabilidade diminui com a distância.

Resposta

letra a) Ψ ( + A ) 2 Ψ ( 0 ) 2 = 0,368

letra b) Ψ ( + A ) 2 Ψ ( 0 ) 2 = 1,83 ⋅ 10 - 2

A probabilidade diminui com a distância.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a energia do ponto zero de um oscilador harmônico com uma partícula de massa de 2,33 × 10 - 26k g e constante de força de 155N.m - 1 .
Admitindo que as vibrações de uma molécula de 35Cl2, são equivalentes às de um oscilador harmônico com a constante de força k = 329N.m - 1 , qual a energia do ponto zero da vibração dessa molécula? A
Calcule a energia do ponto zero de um oscilador harmônico com uma partícula de massa de 5,16 × 10 - 26k g e constante de força de 285N.m - 1 .
Em um oscilador harmônico constituído por uma partícula de massa de 2,88 × 10 - 25k g , a diferença entre os níveis de energia adjacentes é 3,17z J . Calcule a constante de força do oscilador.
Calcule o comprimento de onda de um fóton capaz de excitar uma transição entre níveis de energia vizinhos de um oscilador harmônico cuja massa é de um próton ( 1,0078u ) e constante de força 855Nm - 1