O fundo de um “barco” de aço é uma chapa de aço de . As laterais do barco são feitas de aço com 0,50 cm de espessura. Que altura mínima deve ter a lateral para que o barco flutue em águas perfeitamente calmas?

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!!

Chamando a largura da parte inferior e a largura das folhas laterais como , e as dimensões do barco como sendo a, b e h. O volume total do material que será usado no barco vai ser igual a

o volume de água deslocada será apenas contando pela força flutuante de . Da primeira Lei de Newton, temos que desde o barco não esteja afundando, o peso do material é igual à força de empuxo, ou seja

Isso é nos leva a

Rearranjando para o termo h, nós temos:

Para melhorar o entendimento, vamos utilizar uma imagem

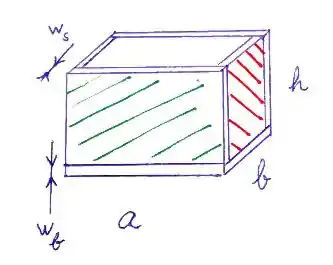
Entenda, olhando para o desenho, teremos que considerar os dois lados, uns dos quais simétrico, não tem comprimento mas sim , devido ao “dobrar os lados”.

Isolando o termo h, temos que