A pressão atmosférica diminui com o aumento da altitude. Vamos descobrir de que maneira isto se dá.
a. Estabeleça um eixo z que aponte para cima, com correspondente ao nível do mar. Suponha que a pressão à altitude z seja p, e que a densidade do ar seja p. Use a equação da pressão hidrostática para escrever uma expressão da pressão em z + dz, altura onde dz é tão pequeno que a densidade não sofre alteração. Sua expressão deverá ser uma função de p , p, dz e, talvez, de algumas constantes. A pressão diminui à medida que você ganha altitude; logo, tenha cuidado com os sinais.
b. Usando a expressão que você obteve no item a, escreva uma expressão para dp, a quantidade pela qual a pressão varia ao se ir de z para z + dz. A pressão está diminuindo; logo, sua expressão deve ser negativa.
c. Você precisa integrar a expressão obtida no item b, mas não pode porque a densidade p não é uma constante. Se a temperatura permanecer constante, que é o que consideraremos, a lei do gás ideal implica que a pressão será diretamente proporcional à densidade, ou seja, , onde e são, respectivamente, os valores da pressão e da densidade ao nível do mar. Use isso para reescrever sua expressão anterior para dp em função de p, dz e de algumas constantes.
d. Agora você dispõe de uma expressão integrável, embora deva primeiro dividi-la por p para obter todos os termos de pressão de um lado da equação. Efetue a integração e use o fato de que em para determinar a constante de integração. Depois, a pressão correspondente à altitude z. O seu resultado final deve ser da forma
e. A grandeza é chamada de escala de altura da atmosfera. Trata-se da altitude na qual , ou cerca de 37% da pressão ao nível do mar. Determine o valor numérico de .
f. A camada mais baixa da atmosfera, chamada de troposfera, tem uma altura de aproximadamente 15.000 m. Esta é a região da atmosfera onde ocorrem os fenômenos climáticos. Acima dela, fica a estratosfera, onde as condições são muito diferentes. Desenhe um gráfico da pressão versus altitude que cubra altitudes de até 15.000 m.
Comentário: Consideramos uma atmosfera de temperatura constante. Na atmosfera real, a temperatura na troposfera diminui com o aumento da altitude. Isso altera a forma como a pressão varia, mas não de maneira muito significativa. O resultado que você obteve constitui uma aproximação razoavelmente boa.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!!
A coluna de ar tem uma área transversal A. Escolhemos a origem do sistema de coordenadas em e denotamos o eixo vertical como o eixo z.
A – A pressão na altura z é igual a , já a pressão na altura é
Com isso, nós temos que
Passo 2
B - A mudança na pressão é igual a O sinal é negativo porque a pressão diminui à medida que z aumenta.
C – Para a lei dos gases ideais, nós temos
O resultado da letra b se torna .
Passo 3
D - para encontrar a pressão p em uma altura z, reescrevemos o resultado da parte (c) como
Integrando os dois lados
Essa integral tem como resultado um logaritmo neperiano, com isso, temos que
Com isso, temos que p é igual a
Onde
Passo 4
E – A altura da escala é
Substituindo os valores, temos que
Passo 5
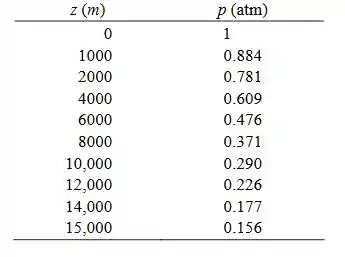
F - Uma tabela mostrando os valores de nos valores selecionados de z seguem.
Resposta
Ei, a resposta está no passo a passo :)