Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 34.Problemas - Ex. 91
A imagem de um objeto situado à esquerda forma-se sobre uma tela a uma distância de à direita da lente. Quando a lente é deslocada para a direita, a tela deve se delocar para a esquerda para que a imagem seja novamente focalizada. Determine a distância focal da lente.
Passo 1
Já que estamos falando sempre de lentes, vamos usar a mesma fórmula nos dois casos:
Cada um dos casos vai te dar um valor de e um de . Vamos fazer um desenho pra representar o primeiro:
E nesse caso a equação fica assim:
E agora vamos deslocar a lente para a direita e a tela para a esquerda:
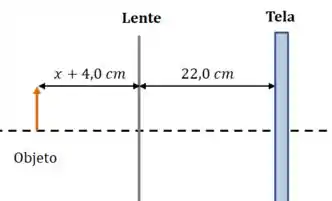
E dessa vez a equação é:
Passo 2
Beleza, agora ficamos com um sistema de duas equações e duas variáveis:
O jeito mais fácil de resolver isso é igualar as duas expressões pelo termo :
Somando as frações:
Agora é só resolver essa equação de segundo grau:
E a única solução positiva é .
Passo 3
Pra finalizar, é só substituir esse valor de em alguma das equações do sistema:
Resposta
A distância focal da lente é .