Um hemisfério sólido de vidro com raio igual a e índice de refração é colocado com sua superfície plana apoiada sobre uma mesa. Um feixe de raios paralelos com seção reta e diâmetro igual a incide verticalmente de cima para baixo e entra no hemisfério através do centro de sua superfície curva. (a) Qual é o diâmetro do círculo de luz que se forma sobre a mesa? (b) De que modo seu resultado depende do raio do hemisfério?
Passo 1
(a) O primeiro passo é fazer um desenho da situação:
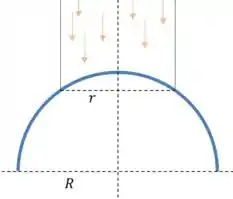
Pra determinar o diâmetro do círculo de luz que é formado sobre a mesa, vamos pensar em um raio de luz que está em uma extremidade do feixe.
Passo 2
Esse raio incide com um ângulo e é refratado com um ângulo :
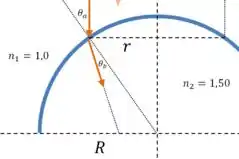
Pela lei de Snell:
E olhando um pouco o desenho, a gente pode achar algumas expressões para os senos de e :
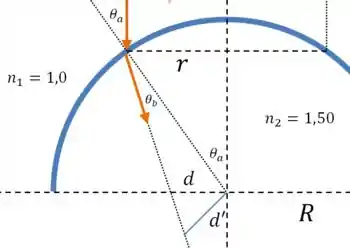
Mas o nosso objetivo final mesmo é calcular aquele , que vai dar o raio do círculo de luz.
Já que na realidade o raio é bem maior do que (nosso desenho é só uma ilustração), os ângulos são bem pequenos, e por isso dá pra fazer essa aproximação aqui:
Então:
Passo 3
Substituindo isso na lei de Snell:
Dá pra cortar o raio da expressão:
Então:
Agora é só substituir os valores numéricos, lembrando de expressar o raio em centímetros:
Esse é o raio do círculo de luz, então o diâmetro é:
Passo 4
Dá uma olhada na expressão que a gente encontrou no passo de cima:
O raio não aparece! Mas ao mesmo tempo, a gente só conseguiu chegar nessa expressão porque o raio era quase dez vezes maior do que . Isso serviu pra fazer aquela aproximação .
Então o raio não afeta o resultado, desde que ele seja grande o suficiente em relação ao raio .
Resposta
(a) O círculo de luz tem de diâmetro.
(b) O raio não afeta o resultado, desde que seja grande o suficiente em relação ao raio do feixe.