Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.Problemas Adicionais - Ex. 81

No instante t = 0 , um elétron com uma energia cinética de 12 ke V que está se movendo no sentido positivo de um eixo x paralelo à componente horizontal do campo magnético B → da Terra passa pelo ponto x = 0 . A componente vertical do campo aponta para baixo e tem um módulo de 55,0 μ T . (a) Qual é o módulo da aceleração do elétron produzida pelo campo B → ? (b) Qual é a distância a que se encontra o elétron do eixo x quando chega ao ponto de coordenada x = 20 c m ?

Passo 1

Como o elétron esta se movimento no sentido positivo do eixo x , a única componente do campo magnético que gera uma força no elétron é a componente vertical, B v . Dessa forma, podemos calcular o módulo da aceleração usando a equação para a força do campo magnético e a segunda lei de newton:

F = q v B v , F = m a

m a = q v B v

a = q v B v m

Além disso, podemos utilizar a relação entre a energia cinética e a velocidade:

K = 1 2 m v 2 → v = k 2 m

Portanto,

a = q B v m 2 k m = q B v 2 k m 3

a = 1,60 × 10 19 55,0 × 10 - 6 2 12 × 10 3 × 1,60 × 10 - 19 9,11 × 10 - 31 3 = 6,3 × 10 14 m / s 2

Passo 2

(b) Bem, como o elétron continua sujeito ao campo magnético sua trajetória é uma circunferência. O raio é dado por:

R = v 2 a

R = 2 k m q B v m 3 2 k = 2 k m q B

R = 2 12 × 10 3 × 1,60 × 10 - 19 9,11 × 10 - 31 1,60 × 10 - 19 55,0 × 10 - 6 = 6,72 m

Dessa forma, vamos desenhar a ideia da trajetória da partícula:

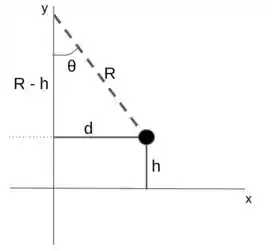
Por relações de triângulo:

d = R s i n θ

R - h = R c o s θ → h = R 1 - c o s θ

h = R 1 - 1 - s i n θ 2 = R 1 - 1 - d R 2

h = 6,72 1 - 1 - 0,20 6,72 2 = 3,0 × 10 - 3 m

Resposta

(a) a = 6,3 × 10 14 m / s 2 (b) h = 3,0 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula alfa se move com uma velocidade v → de módulo 550 m / s em uma região onde existe um campo magnético B → de módulo 0,045 T . (Uma partícula alfa possui uma carga de + 3,2 × 10 - 19 C e u
Um próton está se movendo em uma região onde existe um campo magnético uniforme dado por B → = 10 i ^ – 20 j ^ + 30 k ^ m T . No instante t 1 , o próton possui uma velocidade dada por v → = v x i ^ +
Uma certa partícula subatômica decai em um elétron e um pósitron. Suponha que, no instante do decaimento, a partícula está em repouso em um campo magnético uniforme B → de módulo 3,53 m T e que as tra
Uma partícula penetra em uma região onde existe um campo magnético uniforme, com o vetor velocidade da partícula perpendicular à direção do campo. A Fig. 28-40 mostra o período T do movimento da partí
Qual é o valor do campo magnético uniforme, aplicado perpendicularmente a um feixe de elétrons que se movem com uma velocidade de 1,30 × 10 6 m / s , que faz com que a trajetória dos elétrons seja um