Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.Problemas - Ex. 47
Um instrumento de está pendurado por um cabo vertical no interior de uma espaçonave que está sendo lançada da superfície terrestre. Essa nave parte do repouso e alcança a altitude de em com aceleração constante.
- Desenhe o diagrama de corpo livre para o instrumento nesse período de tempo. Indique qual força é maior.
- Ache a força ache a força que o cabo exerce sobre o instrumento
Passo 1
Sobre esse instrumento (representado por uma caixa no desenho abaixo) estão agindo duas forças: a força peso (vertical para baixo – representada em azul) e a força de tração (é a força com que a nave puxa a caixa – representada em vermelho). Juntando todas essas informações no desenho temos:
A nave (e tudo que está dentro dela)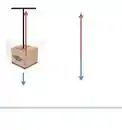
está subindo, com a velocidade aumentando, então a aceleração resultante é para cima. E sabendo que a força resultante segue a direção e sentido da aceleração, então a força resultante aponta para cima. Com isso concluímos que a maior força é a de tração, representada em vermelho.
Passo 2
Para determinar a tração, podemos usar a segunda lei de Newton. A força de tração está apontada para cima, enquanto que a força peso aponta para baixo. Da segunda lei:
Como o movimento é todo na direção vertical, , então podemos equacionar as forças da seguinte forma:
Opa! Só um pouco! Não temos o valor da aceleração! Então antes de tudo, precisamos dela! O problema nos diz que a nave percorre, a partir do repouso , uma distância de , a partir do chão em . Então usando a equação horária da posição para o movimento de queda livre (se você não lembra, dá uma espiadela na nossa plataforma e aproveita para tirar todas suas dúvidas =D) teremos:
Substituindo os valores podemos determinar a aceleração :
Passo 3
Show! Agora que sabemos o valor da aceleração, podemos voltar a equação pra força resultante que achamos no início do passo e descobrir :