Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.1 - Ex. 8
Uma bola grande de um guindaste de demolição é mantida em equilíbrio por dois cabos de aço leves (Figura ). Se a massa da bola for igual a , qual é
a) a tensão no cabo que faz um ângulo de com a vertical?
b) a tensão no cabo horizontal?
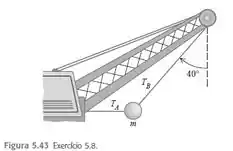
Passo 1
Fala galera! Beleza?! Bora resolver essa questão!
Nós temos uma bola grande de guindaste mantida em equilíbrio por dois cabos e queremos descobrir (a) a tensão no cabo que faz um ângulo de com a vertical e (b) a tensão no cabo horizontal. Além disso, o enunciado nos diz que a massa da bola vale .
Vamos fazer um diagrama de forças para entender melhor o que está acontecendo nesse guindaste:
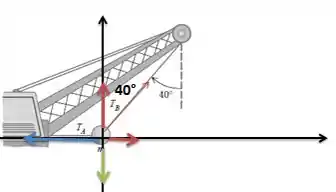
A força está representada em azul, aponta para a esquerda na direção do eixo . A força está representada em vermelho (vetor mais fino) e suas componentes estão também em vermelho, mas em um traço mais gordinho. O peso da bola está representado em verde.
O ângulo que a tensão faz com o eixo vertical é e podemos decompor em termos de seno e cosseno:
Agora que já identificamos todas as forças verticais e horizontais, podemos aplicar a segunda lei de Newton para esse sistema:
Como esse sistema está em equilíbrio a soma de todas as forças deve ser zero:
Assim devemos fazer a soma das forças tanto na componente vertical, quanto na horizontal.
Vamos lá!
Passo 2
Começando pelas forças na horizontal, temos:
Certo? E para a vertical:
Mas o enunciado nos deu quanto vale a massa (), daí podemos calcular o peso e consequentemente a tensão :
Isolando na equação e usando :
Jogando tudo isso na calculadora teremos:
Passo 3
Agora vamos calcular a tensão no cabo . Lembram que deduzimos essa relação:
Agora que sabemos é só substituir:
Valeu, galera! Até a próxima! 😉