47. Um jogador de basquete de consegue saltar verticalmente até no ar, como mostrado na FIGURA P7.47. Analisando a seguinte situação, você poderá compreender como:
O jogador dobra suas pernas até que a parte superior de seu corpo baixe em e depois começa seu salto. Desenhe diagramas de corpo livre separados para o jogador e para o piso quando ele está saltando, antes de seus pés perderem contato com o piso.
Existe uma força resultante sobre o jogador quando ele salta (antes de seus pés deixarem o piso)? Como isso ocorre? Explique.
Com que valor de velocidade o jogador deve sair do piso a fim de saltar verticalmente ?
Quanto vale sua aceleração, considerando que seja constante, quando ele salta (antes de sair do piso)?
Suponha que o jogador salte enquanto está sobre uma balança de banheiro que marca o peso em newtons. Quanto marca a balança antes do salto, durante o salto e depois que seus pés deixaram o piso?
Passo 1
Então galera para esse problema vai ser melhor nós analisarmos cada item em um passo diferente já que o problema é grande e a gente não correr risco de se embolar.
Passo 2
Vamos então começar com o item , antes dos diagramas vamos fazer uma análise da situação das forças que atuam no jogador e no chão em cada momento.
No primeiro momento quando o jogador está agachado temos duas forças agindo nele, a sua força peso e a força normal que o chão aplica nele.
O chão só tem a força de reação que provém da força normal que ele aplica no jogador.
No segundo momento quando o jogador está na eminência de saltar ele faz uma força maior contra o chão para poder saltar, assim o chão reage com uma força normal maior que a força peso do jogador.
O chão ainda tem a mesma reação a força normal que antes, mas agora ela é maior por conta da força que o jogador faz contra o chão.
No terceiro momento o jogador já saiu do chão e não tem mais contato com ele, logo a única força que age no jogador é a força peso.
E no chão não temos mais nenhuma força agindo nele.
Assim temos os seguintes diagramas de corpo livre, primeiro para o jogador.
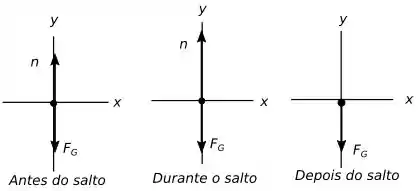
Para o chão temos os seguintes diagramas:
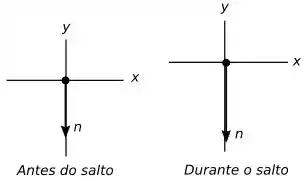
Passo 3
Agora vamos avaliar o item .
Para o jogador sair de uma velocidade inicial igual a zero e subir com uma velocidade ele precisa de uma aceleração e segundo a lei de Newton temos uma força resultante que aponta para cima.
Então a normal do jogador deve ser maior que sua força peso para que tenhamos uma resultante para cima e ele consiga sair do chão e isso ocorre porque o jogador aplica uma força maior que sua força peso no chão.
Aí o chão reage com uma força de reação maior que a força peso do jogador.
Passo 4
Agora vamos pensar no item . Vamos usar a seguinte equação da cinemática para encontrar a velocidade inicial do jogador para que ele suba .
Onde a nossa aceleração é , a posição final é e temos uma velocidade final . Assim temos:
Já sabemos o valor de , assim:
Passo 5
Agora vamos para o item .
Agora para achar a aceleração que o jogador deve ter para ter uma velocidade de saída do chão de vamos usar a mesma equação do passo anterior, assim temos:
Onde dessa vez teremos e que é o quanto ele se curva para saltar, assim temos o seguinte:
Então temos que:
Passo 6
Agora vamos para o item .
Para fazermos esse item temos que saber que uma balança convencional mede na verdade é a força normal, então para saber quanto a balança marca devemos saber o valor da normal quando o jogador faz força para pular.
Assim vamos fazer a análise do jogador usando a segunda lei de newton.
Para antes do salto temos o seguinte:
Então temos:
Agora para o momento que o jogador está fazendo força para saltar temos o seguinte:
Agora usando o valor da aceleração que achamos no item , temos:
Então temos:
Isso é o que a balança mede quando o jogador está preste a pular.
Depois que o jogador pulou não tem mais nada em contato com a balança, assim sua nova medida é zero.
Resposta
Existe sim uma força resultante.
Antes do salto:
Durante o salto:
Depois do salto: