Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 1
1. || Como parte de um sério projeto científico, você deseja lançar um
modelo de foguete de 800 g verticalmente para cima e atingir um
alvo que se move horizontalmente quando este passa 30 m acima
do ponto de lançamento. O motor do foguete gera um empuxo
constante de 15,0 N. O alvo está se aproximando com uma velocidade
de 15 m/s. A que distância horizontal entre o alvo e o foguete
você deveria lançá-lo?
Passo 1
Galera o mais importante nesse tipo de exercícios é entender o que esta acontecendo, sempre façam desenhos e tentem entender os movimentos, porque sem isso é muito fácil se confundir e as vezes entender uma coisa nada a ver com o que esta sendo pedido. Então vamos as desenho:
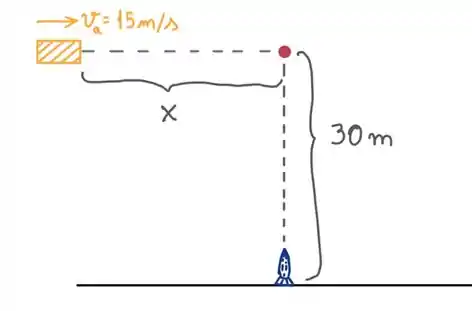
Aquele ponto vermelho é onde eles vão se bater.
O foguete, que desenhei de azul, tem que subir até atingir o alvo.
E o alvo, em amarelo, tem que percorrer uma distância , que queremos descobrir, até chegar no ponto vermelho.
Quando analisamos dois movimentos diferentes precisamos achar relações entre eles, pois sem isso não conseguimos relacionar uma coisa com a outra. Então, o que que esses movimentos tem em comum?
O tempo, ele vai ser o mesmo para os dois. Com isso já podemos montar as equações, vamos lá.
Passo 2
O alvo se move com uma velocidade constante para a direita. Ele percorre uma distância em um tempo e sua velocidade é de . Sabemos que a velocidade, quando constante, pode ser escrita assim:
No nosso caso:
Então precisamos do tempo que demorou para descobrir essa distância.
Beleza, desse movimento não da pra tirar mais nada. Vamos pensar na subida do foguete.
Passo 3
Ele tem uma força constante empurrando ele para cima, mas também tem seu peso puxando ele para baixo. Como sabemos essas duas forças vamos usar a 2ª lei ne Newton, para descobrirmos a aceleração desse foguete:
A força do motor é igual a , a massa é (cuidado com a unidade de medida) e a gravidade é :
Isolando a aceleração:
Belezaaaa, agora vamos para as equações da cinemática pra descobrir o tempo que demorou pra isso ai bater no quadradinho amarelo.
Nossa posição inicial é o chão, então vamos falar que .
Sabemos a altura final dele: .
Ele tá paradinho no chão antes de sair voando, então .
E a aceleração acabamos de encontrar. Jogando tudo isso ai na equação:
Isolando o .
Passo 4
Agora é só substituir o tempo na equaçãozinha que descobrimos no Passo 2 e correr pro abraço.
E é isso ai.