A luz emitida pelo elemento X passa por uma rede de difraçăo com 1200 linhas/mm. O padrăo de difraçāo é observado em uma tela posicionada atrais da rede. As franjas brilhantes sâo vistas na tela a distâncias de e em relaçăo ao máximo central. Nenhuma outra franja ć observada.a. Qual é o valor de correspondente a cada um desses comprimentos de onda difratados? Explique por que apenas um valor possivel de ser visto.b. Quais sāo os comprimentos de onda luminosa emitidos pelo Elemento X"?
Passo 1
E aiii gente, tudo bom com vocês?
Então vamos resolver essa questão bem legal aqui e passo a passo pra gente tirar 10 na provinha!
Vamo lá!
Letra a:
Uma afirmação importante é que as linhas são vistas na tela. Isso significa que a luz é a luz visível, na faixa de . Podemos determinar onde todo o espectro visível cai na tela para diferentes valores de . Fazemos isso encontrando os ângulos nos quais a luz de e a luz de são difratadas. Nós então usamos para encontrar suas posições na tela, que está a uma distância .
O espaçamento da fenda é:
Para :
Para :
Para o comprimento de onda de em ,
Que não é definido, então .
Nós vemos que a luz visível difratada em cairá na faixa de e que a luz visível difratada em cairá no intervalo . Esses intervalos não se sobrepõem, portanto, podemos concluir que as linhas de difração observadas são todas .
Passo 2
Letra b:
Para determinar os comprimentos de onda, primeiro encontramos o ângulo de difração da posição observada usando:
Este ângulo é então usado na equação da rede de difração para o comprimento de onda com .
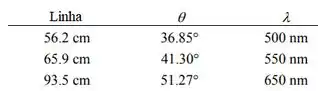
Resposta
- m=1
- Ver resposta