Mercúrio é despejado em um tubo em forma de U, como mostra a Figura P15.17a. O braço esquerdo do tubo tem área transversal de 10,0 cm², e o braço direito tem área transversal de 5,00 cm². Cem gramas de água são então despejados no braço direito, como mostra a Figura P15.17b. (a) Determine o comprimento da coluna de água no braço direito do tubo U. (b) Sendo a densidade de mercúrio 13,6 g/cm³, que distância h o mercúrio sobe no braço esquerdo?

Fala aí! Dá só uma olhada na imagem a que o enunciado se refere:

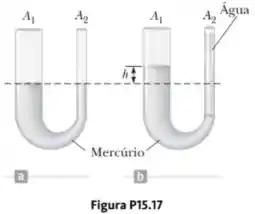
Vamos pensar na primeira parte dessa questão, se liga, quando ele pergunta o comprimento da coluna de água no braço direito do tubo, basicamente, podemos pensar em que altura teria uma coluna de água que pesasse 100 g em uma garrafa de área transversal de 10,0 cm². Olha como vamos calcular isso: o volume de um cilindro é dado pela área da base vezes a altura

Nós conhecemos a área da base e sabemos a densidade da água. Então, como também sabemos a massa da água, podemos encontrar seu volume, aí basta substituir os valores nessa equação acima e resolver para H.

Então:

Essa é a altura da coluna de água.