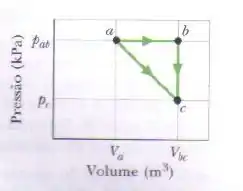
Um mol de um gás ideal diatômico vai de a a c ao longo da trajetória diagonal na figura. A escala do eixo vertical é definida por p a b = 5,0k P a e p c = 2,0k P a , e a escala do eixo horizontal é definida por V b c = 4,0m 3 e V a = 2,0m 3 . Durante a transição, (a) qual é a variação da energia interna do gás e (b) qual é a energia adicionada ao gás na forma de calor? (c) Que calor é necessário para que o gás vá de a a c ao longo da trajetória indireta a b c ?

(a) Δ E a c = - 5,0.10 3J .(b) Q = 2,0.10 3J .(c) Q = 5,0.10 3J .

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 19.7 - Ex. 44

Um mol de um gás ideal diatômico vai de a ao longo da trajetória diagonal na figura. A escala do eixo vertical é definida por e , e a escala do eixo horizontal é definida por e . Durante a transição, (a) qual é a variação da energia interna do gás e (b) qual é a energia adicionada ao gás na forma de calor? (c) Que calor é necessário para que o gás vá de a ao longo da trajetória indireta ?

Passo 1

(a) Muito cuidado aqui! O gás é diatômico então as fórmulas sofrem algumas modificações. Por exemplo, pra calcular a energia interna, nós usamos essa fórmula aqui:

Só que no caso do gás diatômico o calor específico molar é:

Ou seja:

Só que como o gráfico só fala de pressão e volume, vamos usar a lei dos gases ideais pra fazer essas grandezas aparecerem aí no meio:

Beleza, e aí a variação da energia interna entre os estados e vai ser:

Ótimo, agora é só substituir os valores:

Passo 2

(b) E agora, qual a quantidade de calor recebida pelo gás?

Bom, calcular o calor a partir do gráfico é mais complicado, mas dá uma olhada na primeira lei da termodinâmica:

Como nós já sabemos a variação da energia interna, só falta saber o trabalho realizado pelo gás nesse ciclo e já vamos saber o calor.

Mas cuidado! Só queremos o calor adicionado no trajeto que vai do ponto ao ponto , ou seja, através daquela linha inclinada ali no gráfico, então é o trabalho que nos interessa vai ser a área embaixo daquela linha.

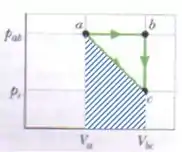
E então:

Resolvido.

Passo 3

(c) Bom, queremos achar o calor de novo, mas agora no caso em que o gás faz o outro caminho entre e . Aquela fórmula de antes continua valendo:

A variação da energia interna é a mesma, lembre sempre disso: a variação da energia interna não depende do caminho, só dos estados inicial e final.

E pra encontrar o trabalho é só fazer embaixo do gráfico de novo:

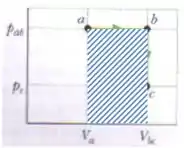
Beleza, agora é só voltar na fórmula de cima:

Resposta

(a) .

(b) .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cubo de 6,0.10 - 6m de aresta e emissividade0,75 , à temperatura de - 100 ° C , flutua no espaço sideral onde a temperatura é - 150 ° C . Qual é a taxa líquida de transferência da radiação térmica

O calorímetro de fluxo é um dispositivo usado para medir o calor específico dos líquidos. O líquido que passa pelo calorímetro, com uma vazão conhecida, recebe energia, na forma de calor, a uma taxa c

Um liquido é agitado irregularmente em um recipiente bem isolado e, portanto, sua temperatura aumenta. Considere i liquido o sistema. a) Ocorre transferência de calor? Como você pode garantir? b) Exis

Você fecha o bico de uma bomba de pneu de bicicleta e aperta o êmbolo rapidamente, de modo que o ar lá dentro seja comprimido à metade do volume original. Suponha que o ar se comprote como um gás idea

Um sonho típico contém 2,0g de proteína, 17,0 g de carboidrato e 7,0 g de gordura. Os valores médios de energia alimentícia dessas substancias são 4,kcal/g para a proteína e os carboidratos e 9,0 kcal