Mostre que, para um átomo de Thomson, um elétron que se move em uma órbita circular estável gira com a mesma frequência que teria caso oscilasse ao longo de um diâmetro em torno do centro.
Passo 1
Fala galerinha, beleza?
Primeiro você lembrar que o átomo de Thomson consiste em uma distribuição uniforme de carga positiva (que podemos supor esférica e com um raio ) e um elétron orbitando o centro da esfera (com um raio ):
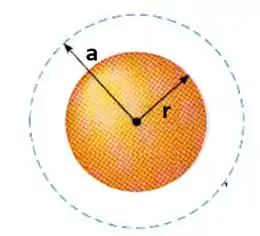
A carga do elétron é e a carga total da esfera positiva de raio é , de modo que a carga total é nula. Para encontrar o campo elétrico sobre o elétron, consideramos a lei de Gauss:
Vamos considerar a esfera de raio como superfície gaussiana, já que é nela que o elétron vai estar:
Passo 2
Qual é a carga dentro dessa esfera de raio ? O truque é considerar que na esfera toda de volume temos uma carga , de modo que dentro da esfera de raio com volume devemos ter a carga :
Portanto,
Desta forma, a força centrípeta que atua sobre o elétron é
O sinal de menos indica que a força aponta para dentro, como deve ser para uma força centrípeta. Assim, temos
Isso nos dá a frequência angular de rotação do elétron.
Passo 3
Agora vamos considerar a situação em que o elétron oscila harmonicamente em torno do núcleo. Observe que a força pode ser escrita na forma da lei de Hooke:
Você deve saber que para forças desse tipo, o movimento é harmônico com frequência angular dada por
Note que ela coincide com o resultado do passo 2. Isso prova o que o enunciado pediu: os dois movimentos têm a mesma frequência!
Resposta
Demonstração.