Supondo que se pode colocar uma quantidade de hidrogênio com número de massa três (o trítio) suficiente para exames espectroscópicos em um tubo contendo hidrogênio comum, determine a separação entra a primeira linha de Balmer para o hidrogênio normal e a que seria observada.
Passo 1
Fala galerinha, beleza?
A seguir reproduzimos todos os decaimentos envolvendo os quatro primeiros níveis de energia do átomo de hidrogênio:
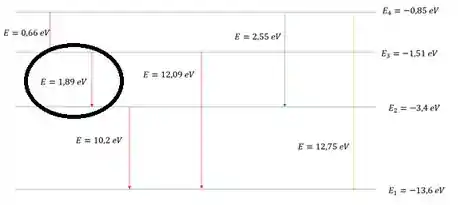
A transição destacada corresponde a linha : a transição de menor energia na série de Balmer (que termina em ). Portanto, a energia do fóton da primeira linha de Balmer para o hidrogênio comum é
A pergunta que devemos responder é: o que acontece se considerarmos o trítio?
Passo 2
Volte para a equação (4-26c) do livro. A energia é dada por
Podemos multiplicar e dividir a equação pela massa do elétron:
Sabemos que
Assim, para próton, temos
A questão é analisar o quanto a correção vai mudar os níveis de energia.
Passo 3
Lembre-se que a massa reduzida é dada por
Para o hidrogênio comum, , onde é a massa do próton. Já para o trítio, temos
Assim,
A energia do fóton emitido no átomo de hidrogênio é
Analogamente, para o trítio:
Com isso, podemos escrever
Para a transição da linha , temos e . Além disso, temos :
Assim,
Falta calcular o termo entre parênteses!
Passo 4
Lembre-se que
Assim,
Como , temos
Assim,
Ou ainda,