Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 19.1 - Ex. 76
Mostre que o coeficiente de desempenho de uma máquina de Carnot funcionando como refrigerador está relacionado ao rendimento de uma máquina de Carnot operando entre as mesmas duas temperaturas por
Passo 1
Olá! Então, o que queremos aqui? Cara, ele pediu para provarmos que
Sendo que é a temperatura de um reservatório frio e a temperatura de um reservatório quente.
é o rendimento de uma máquina de Carnot atuando entre esses reservatórios e é o coeficiente de desempenho de um refrigerador atuando também entre essas mesmas temperaturas.
Então a ideia é ver o funcionamento da máquina e do refrigerador, e as expressões que os descrevem, relacionar as grandezas que ele deu e provar isso aí. Bora lá!
Passo 2
Legal galera, vamos começar analisando o coeficiente de desempenho para um refrigerador. Ele tem essa expressão
é o trabalho que ele recebe e é o calor que sai do reservatório frio.
Agora precisamos relacioná-lo à eficiência do ciclo de Carnot. Então vamos manipular um pouco esta equação.
Vamos começar lembrando o esqueminha do refrigerador:
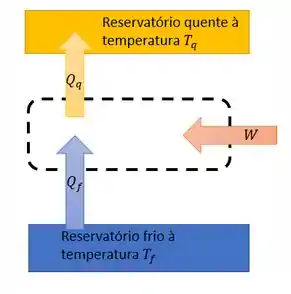
O trabalho e o calor da fonte fria entram e o calor sai para a fonte quente, então podemos escrever essa expressão:
Isolando
Substituindo na expressão de
Vamos guardar esta informação!
Passo 3
Nós queremos relacionar a equação do passo 1 com a eficiência da máquina térmica. Vamos lembrar como se calcula:
Então, se nós dividirmos todos os termos da equação do CD por acharemos CD em função da eficiência:
Já está ganhando forma, não é?
Passo 4
Quando falamos em ciclo de Carnot, existe outra forma de se calcular a eficiência:
Substituindo no termo à direita:
Concluindo:
Prontinho!
Resposta
Demonstração nos passos