Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 28.1 - Ex. 57
Um longo fio cilindrico tem raio igual a 2,0 cm e conduz uma corrente de 80 A uniformemente distribuida ao longo da area da secao transversal.Determine a energia magnetica por unidade de comprimento no interior do fio.
Passo 1
E aí galera, vamos para a resolução de mais um exercício!!
Considere um anel cilíndrico de espessura em um raio . Podemos usar sua definição para expressar a energia magnética total dentro do anular cilíndrico e dividir ambos os lados desta expressão pelo comprimento do fio para expressar a energia magnética por unidade de comprimento . A integração desta expressão nos dará a energia magnética por unidade de comprimento dentro do fio.
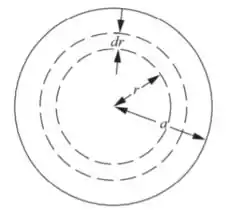
Expresse a energia magnética dentro do anular cilíndrico:
Divida ambos os lados da equação por para expressar a energia magnética por unidade de comprimento :
Passo 2
Use a lei de Ampère para expressar o campo magnético dentro do fio a uma distância de seu centro:
onde é a corrente dentro do cilindro de raio .
Como a corrente é uniformemente distribuída sobre a área da seção transversal do fio:
Substitua para obter:
Substituindo por na equação e simplificando, temos:
Passo 3
Vamos integrar de a para obter:
Substitua os valores numéricos e avalie :
Observações: Observe que a energia magnética por unidade de comprimento é independente do raio do cilindro e depende apenas da corrente total.