Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 28.1 - Ex. 39

Um anel retangular de 10 cm por 5,0 cm(Figura 28-46) com resistencia de 2,59se move a uma rapidez.constante de atraves de uma regiao que tem um campo magnetico uniforme de 1,7 T apontando para fora da pagina,como mostrado.A frente do anel entra na regiao do campo no instantet 0.(a)Faca um gráfico do fluxo atraves do anel como funcao do tempo.(b)Faca um gratico da fem induzida e da corrente do anel como funcoes do tempo. Despreze qualquer auto-indutancia do anel e construa seus gráficos incluindo o intervalo

Passo 1

E ai galera!! Vamos começar aqui essa questão?? Vai ser bem rápido e eu garanto que vocês vão entender!!

Precisamos determinar quanto tempo leva para o anel entrar completamente na região em que há um campo magnético, quanto tempo ele fica na região e quanto tempo leva para deixar a região. Uma vez que conhecemos esses tempos, podemos usar sua definição para expressar o fluxo magnético em função do tempo. Podemos usar a lei de Faraday para encontrar a fem induzida em função do tempo.

Letra a:

Encontre o tempo necessário para o anel entrar na região onde há um campo magnético uniforme:

t = l lado do anel v = 10 c m 2.4 c m / s = 4.17 s

Deixando w representar a largura do anel, expresse e avalie ϕ m para 0 < t < 4.17 s :

ϕ m = N B A = N B w v t = ( 1.7 T ) ( 0.050 m ) ( 0.024 m / s ) t = ( 2.04 m W b / s ) t

Encontre o tempo durante o qual o anel está totalmente na região onde há um campo magnético uniforme:

t = l lado do anel v = 10 c m 2.4 c m / s = 4.17 s

ou seja, o anel começará a sair da região quando t = 8.33 s .

Expresse ϕ m para 4.17 s < t < 8.33 s :

ϕ m = N B A = N B l w = ( 1.7 T ) ( 0.10 m ) ( 0.050 m ) = 8.50 m W b

A extremidade esquerda do anel sairá do campo quando t = 12.5 s . Expresse ϕ m para 8.33 s < t < 12.5 s :

ϕ m = m t + b

onde m é a inclinação da linha e b é a interceptação de ϕ m .

Para t = 8.33 s e ϕ m = 8.50 m W b :

8.50 m W b = m 8.33 s + b                     ( 1 )

Para t = 12.5 s e ϕ m = 0 :

0 = m 12.5 s + b                 ( 2 )

Resolva as equações (l) e (2) simultaneamente para obter:

ϕ m = - ( 2.04 m W b / s ) t + 25.5 m W b

O anel estará completamente fora do campo magnético quando t > 12.5 s e:

ϕ m = 0

Veja o seguinte gráfico de ϕ m ( t )

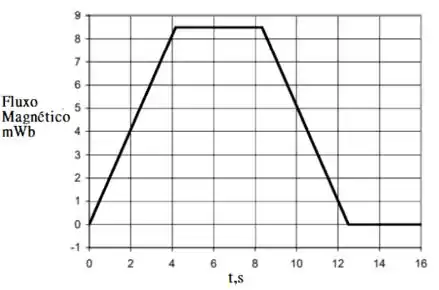
Passo 2

Letra b:

Usando a lei de Faraday, relacione a fem induzida ao fluxo magnético:

ε = - d ϕ m d t

Durante o intervalo 9 < t < 4.17 s :

ε = - d d t [ ( 2.04 m W b / s ) t ] = - 2.04 m V

Durante o intervalo 4.17 s < t < 8.33 s :

ε = - d d t [ 8.50 m W b ] = 0

Durante o intervalo 8.33 s < t < 12.5 s :

ε = - d d t [ ( - 2.04 m W b / s ) t + 25.5 m W b ] = 2.04 m V

Para t > 12.5 s :

ε = 0

A corrente em cada um desses intervalos é dada pela lei de Ohm:

I = ε R

Veja o seguinte gráfico de ε ( t ) :

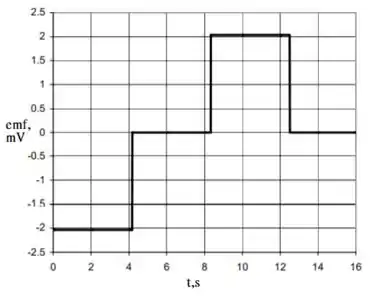
Veja também o seguinte gráfico de I ( t )

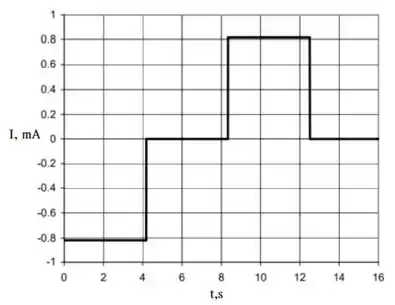
Resposta

  1. Ver resolução
  2. Ver resolução
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O fluxo através de um anel é dado por ϕ m = 0,10 t 2 - 0,40 t , onde ϕ m está em webers e t em segundos. a Esboce gráficos do fluxo magnético e da fem induzida como função do tempo. b Em que instante(
O fluxo através de um anel é dado por ϕ m = 0,10 t 2 - 0,40 t , onde ϕ m está em webers e t em segundos. a Determine a fem induzida como função do tempo. b Determine ϕ m e ε em t = 0 ,t = 2,0 s ,t = 4
Seu amigo decide gerar potência elétrica girando uma bobina de 100000 voltas de fio em torno de um eixo no plano da bobina que passa pelo seu centro. A bobina é perpendicular ao campo magnético da Ter
Uma bobina com N voltas e área A está suspensa no teto por um fio que fornece um torque restaurador linear com uma constante de torção k . As duas extremidades da bobina estão conectadas entre si, ela