Um objeto de 1,0 cm de altura encontra-se a 110 cm de uma tela. Uma lente divergente com distância focal de -20 cm está posicionada 20 cm à frente do objeto. Quais são a distância focal e a distância até tela de urna segunda leme que produz uma imagem bem focada com 2,0 cm de altura nessa tela?
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!!
Primeiramente, vamos encontrar a imagem da lente divergente, usando a equação:
Substituindo os valores, nós temos:
Com isso, é igual a:
Agora, o passo vai ser encontrar a ampliação dessas lentes divergentes, que é feito pela seguinte fórmula:
Fazendo para as lentes convergentes, nós temos a seguinte relação:
E para a ampliação:
Com isso, a ampliação total é dada por:
Passo 2
Depois desses processos, o diagrama fica da seguinte forma:
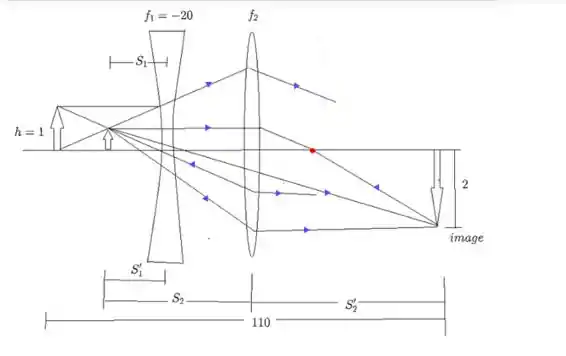
Passo 3
Agora, é encontrar os valores de e , para isso usaremos daquela relação , então, temos:
Substituindo no termo...
Logo, (não é o coração!) vai ser igual a:
Com isso, será igual a:
Passo 4
Com isso, vamos usar a equação da lente para encontrar a distância focal, logo:
Com isso, será igual a: