Os raios que saem do sistema óptico de dois componentes da FIGURA PD24.50 produzem duas imagens distintas do objeto de 1,0 cm de altura.
a. Quais são a posição (em relação à lente), a orientação e a altura de cada imagem formada?
b. Desenhe dois diagramas de raios, um para cada imagem que mostrem como são formadas as imagens
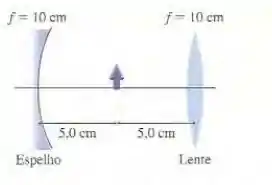
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!!
Vamos lá, os raios que saem do objeto podem passar direto pela lente e isso cria uma imagem, mas os raios também podem refletir do espelho e em seguida, passar pela lente. Temos que usar a equação de lente fina e as equações do espelho curvo, bem como as ampliações para assim, encontrar a posição e o tamanho das imagens.
Depois dessa introdução acerca do problema, vamos encontrar primeiramente a posição da imagem que é criada quando os raios passam apenas através da lente.
Manipulando essa equação da lente fina, temos que é igual a:
Agora, substituindo os termos, temos:
Logo, esta imagem é criada no espelho que fica à esquerda que fica 10 centímetros à esquerda da lente.
Passo 2
Seguindo o processo, calculamos o tamanho e a orientação da imagem, com isso nós temos:
Fazendo as manipulações, nós temos:
Fazendo a substituição, nós temos:
A interpretação desse resultado é que a imagem é vertical e tem 2 centímetros de altura. Agora o processo é encontrar a posição da imagem que é criada quando os raios refletem no espelho e saem pela lente (Para isso, vamos utilizar a equação da lente fina de novo 😊)
Com isso, fazendo as manipulações, temos que é igual a:
Com isso, é igual a:
Como o referencial é o ponto anterior, que está 10 centímetros à esquerda, essa nova imagem vai estar a 20 cm à esquerda.
Passo 3
Agora, vamos encontrar a posição da imagem na lente:
Com isso, temos que é igual a:
Logo, a imagem está 20 centímetros a direita da lente. Agora, finalmente vamos calcular o tamanho e a orientação da imagem para a ampliação total:
Vamos substituir os termos, da seguinte forma:
Com isso, fazendo as manipulações, o vai ser igual a:
Substituindo os valores, temos que:
Portanto, a imagem está invertida e 2 centímetros acima.
Passo 4
O diagrama para quando os raios saem através das lentes é dado por:
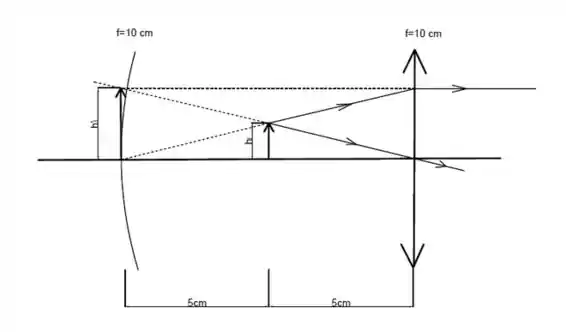
E no caso da reflexão do espelho quando os raios atravessam as lentes é dado por:
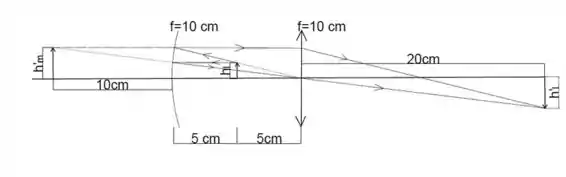
Resposta
Ei, a resposta está no passo a passo :)