Um objeto de 1,0 cm de altura encontra-se 2,5 cm à esquerda de uma lente divergente com distância focal de -2,5 cm. Outra lente, convergente e com distância focal de 5,0 cm. encontra-se a uma distância d à direita da primeira lente.
a. Para que valor de ‘d’ a imagem estará no infinito?
b. Desenhe um diagrama de raios para esta situação.
c. Qual é o tamanho angular da imagem vista olhando-se através da lente convergente?
d. Qual é o aumento angular dessa lente de aumento composta de duas lentes?
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!!
Quando o objeto da lente convergente está em seu foco, a imagem daquele objeto está no infinito, lembre-se de como qualquer raio vindo do foco irá refratar paralelamente ao eixo óptico, o que cria a imagem no infinito. Primeiro, temos que encontrar a posição da imagem da lente divergente para que possamos colocá-lo no foco do ponto convergente, e, a partir disso, encontrar a separação ‘d’.
A posição da imagem em uma lente divergente é dada por:
Fazendo a manipulação para encontrar s’, temos:
A imagem da lente divergente é criada à esquerda dela, com isso temos a seguinte relação:
Substituindo os valores, temos:
E o diagrama é mais ou menos dessa forma aqui:
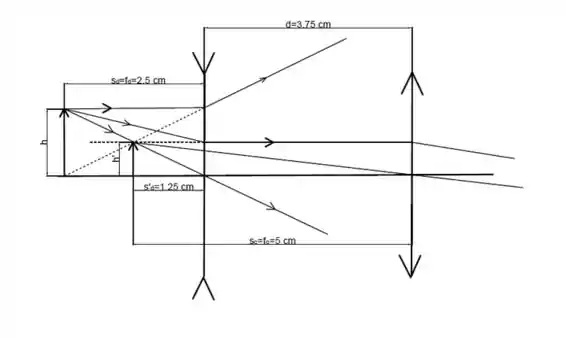
Passo 2
O tamanho angular do objeto pode ser calculado da seguinte fórmula:
No nosso caso, estamos usando lentes divergentes, sendo que estas estão no foco das lentes convergentes que usamos, com isso, temos:
Primeiro, agora, vamos calcular a altura da imagem das lentes divergentes, logo:
O termo h’ é dado por:
Agora nós podemos calcular o tamanho angular do objeto olhando sob a ótica das lentes convergentes.
Passo 3
Calculamos o tamanho angular do objeto visto usando nosso sistema óptico e tudo o que temos que fazer é encontrar o tamanho angular desse objeto se formos olhar para com nossos olhos. Colocamos o objeto no ponto próximo e obtemos:
A ampliação angular do nosso sistema é igual a: