Quais são a posição, a altura e a orientação da imagem final? Expresse a posição como uma distância à direita ou à esquerda da lente.
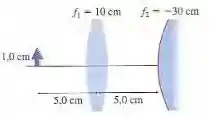
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!
Pelo enunciado, temos que a imagem da lente é o objeto esférico, nós podemos usar isso para resolver algumas coisas, primeiro para resolver a posição da imagem e um segundo ponto resolver a posição final da lente. Essa primeira lente vai ampliar a imagem em um fator , depois disso, o espelho esférico irá aumentar ainda mais pelo fator de . Então a nossa querida imagem final será algo do tipo:
Passo 2
A posição da imagem da lente é:
Fazendo as manipulações, temos que s’ é igual a:
Substituindo os valores, temos:
Logo, temos a seguinte interpretação: a imagem está no mesmo lado do objeto, e está a uma distância de 10 centímetros das lentes.
Passo 3
A imagem da lente está a quinze centímetros do espelho, nesse caso, vamos usar como referencial o espelho esférico, com isso nós temos:
Fazendo as manipulações, temos que s’ é igual a:
Agora é substituir:
Com isso, a imagem será criada a dez centímetros à direita do espelho, ou quinze centímetros á direita das lentes. Com isso, já podemos calcular a altura da imagem
Desenvolvendo, temos:
Agora, vamos substituir as variáveis:
A imagem está a 1,33 centímetros acima.
Resposta
Ei, a resposta está no passo a passo :)