Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 32.1 - Ex. 45
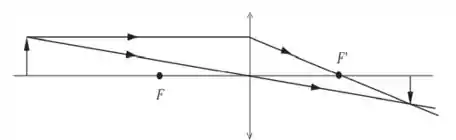
a) Um objeto que tem 3,00 cm de altura é colocado a 25,0 cm em frente a uma lente delgada que tem um poder igual a 10,0 D. Desenhe um diagrama de raios para determinar a posição e o tamanho da imagem e verifique seus resultados usando as equações das lentes delgadas.
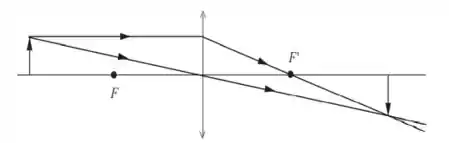
b) Repita a parte a) se o objeto é colocado a 20,0 cm em frente à lente.
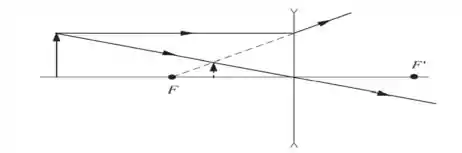
c) Repita a parte a) para um objeto colocado a 20,0 cm em frente a uma lente delgada que tem um poder igual a -10,0 D.
Passo 1
Vamos começar no item a), meus queridos:
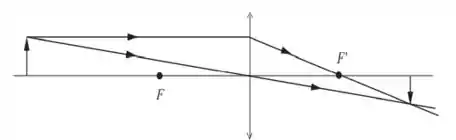
A imagem é real, invertida e menor.
Para conferir se os cálculos reiteram as informações dadas pela análise da imagem vamos usar algumas equações: usaremos a equação do poder (para encontrar a distância focal), a equação das lentes (para encontrar a posição da imagem) e, por fim, a igualdade da ampliação das imagens .
Vamos isolar
Onde:
Agora, nos resta substituir os valores fornecidos pela questão!
Como , sabemos que a imagem é, de fato, real.
Agora, vamos saber se a imagem é, de fato, menor e invertida.
Substituindo os valores fornecidos:
Comparando:
Como a imagem é menor.
E, também, como é invertida.
Passo 2
Vamos pro item b).
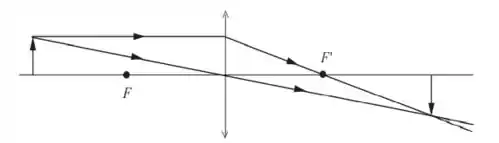
A imagem é real, invertida e, aparentemente, igual.
Vamos isolar
Onde:
Agora, nos resta substituir os valores fornecidos pela questão!
Como , sabemos que a imagem é, de fato, real.
Agora, vamos saber se a imagem é, de fato, igual e invertida.
Substituindo os valores fornecidos:
Comparando:
Como a imagem é igual.
E, também, como é invertida.
Passo 3
Por fim, o item c):
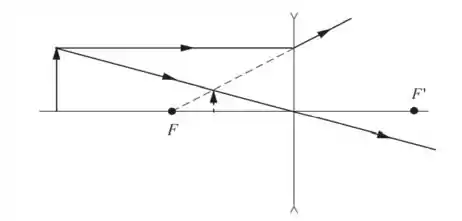
A imagem é virtual, direita e menor.
Vamos isolar
Onde:
Agora, nos resta substituir os valores fornecidos pela questão!
Como , sabemos que a imagem é, de fato, virtual.
Agora, vamos saber se a imagem é, de fato, igual e invertida.
Substituindo os valores fornecidos:
Comparando:
Como a imagem é menor.
E, também, como é direita.
Resposta
