Ampliação angular. Ao deduzir a equação 34.22 para a ampliação angular de uma lupa, supusemos que o objeto estivesse no foco da lupa, de modo que a imagem virtual se formasse no infinito. Em vez disso, suponha que o objeto seja colocado em uma posição tal que a imagem virtual se forme no ponto próximo de um observador médio a uma distância de , o ponto mais próximo que o observador pode focalizar um objeto. (a) onde o objeto deve ser colocado para se obter esse resultado? Fornceça a resposta em termos da distância focal da lupa. (b) Qual é o ângulo que um objeto de altura subtende na posição encontrada no item (a)? (c) Calcule a ampliação angular para o objeto na posição encontrada no item (a). O ângulo é o mesmo que o indicado na Figura 34.51a, visto que ele se refere a uma observação do objeto sem usar a lupa. (d) Para uma lente convexa com , qual é o valor de para o objeto na posição encontrada no item (a)? Quantas vezes esse valor de é maior do que o valor encontrado quando a imagem se forma no infinito? (e) Na descrição do microscópio composto feita na Seção 34.8, afirmamos que em um instrumento projetado adequadamente, a imagem real formada pela objetiva deve se encontrar na parte interna entre o primeiro foco e a ocular, em um ponto quase sobre o foco da ocular. Qual é a vantagem de a imagem formada pela objetiva estar quase sobre o foco da oscular em relação à formação da imagem exatamente sobre o foco da ocular? O que ocorreria se a imagem se formasse na parte externa, em um ponto situado quase sobre o foco ?

Equação 34.22:

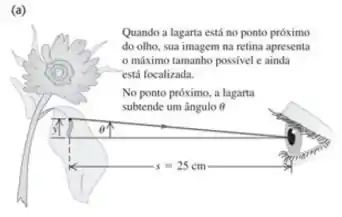
Figura 34.51a:

(b) Se um objeto está a de distância e mede uma altura , o ângulo vai seguir essa fórmula aqui:

Usando a fórmula do passo 1:

Então o ângulo é:

E se esse argumento dentro do arcotangente for bem pequeno, a gente pode usar aquela velha aproximação :

(c) Lembra da fórmula da ampliação angular ? É bem parecida com a ampliação transversal com que estamos acostumados:

Pela fórmula do item anterior:

E o ângulo que o objeto ocupa no campo de visão é mais fácil de calcular, já que ele tem altura e está a de distância:

Então:

(d) Nesse item a gente só precisa retomar a fórmula que foi demonstrada no item (c):

E substituir com :

Quando a imagem se forma no infinito, a amplificação teria que ser calculada com a fórmula de sempre:

Então podemos comparar os dois:

Ou seja, quando a imagem se forma no infinito a amplificação é vezes maior.

(e) A vantagem de fazer isso é que a imagem real formada pela objetiva pode agir como um objeto para a ocular. E depois esse “objeto” produz uma imagem virtual e aumentada.

Se a imagem gerada pela objetiva ficasse do lado de fora, a imagem gerada pela ocular seria real e menor.