Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Griffiths - Mecânica Quântica- Ed: 2º - Capítulo 2.Problemas - Ex. 22 c

O pacote de onda gaussiano. Uma partícula livre tem como função de onda inicial:

Ψ x , 0 = A e - a x 2

Em que A e a são constantes ( a é real e positivo).

c) Calcule Ψ x , t 2 . Dê sua resposta em termos da quantidade

ω = a 1 + 2 ℏ a t m 2

Esboce | Ψ x , t ​ 2 (como uma função de x ) em t = 0 , e novamente para t bastante grande. Qualitativamente, o que acontece com Ψ 2 no decorrer do tempo?

Passo 1

O item c) vai pedir um cuidado maior com as contas para   | Ψ x , t ​ 2 . Dessa maneira, vamos definir a quantidade θ = 2 ℏ a t / m para facilitar nossa vida. Assim vamos às contas:

| Ψ x , t ​ 2 = 2 a π   e - a x 2 1 + i θ   e - a x 2 1 - i θ   1 + i θ 1 - i θ

O expoente de e fica:

- a x 2 1 1 + i θ + 1 1 - i θ = - a x 2   2 1 + θ 2

Portanto, a densidade de probabilidade fica:

Ψ x , t 2 = 2 a π   e - 2 a x 2 1 + θ 2 1 + θ 2

Assim, como ω = a / ( 1 + θ 2 ) , ficamos com:

Ψ x , t 2 = 2 π     ω   e - 2 ω 2 x 2

Passo 2

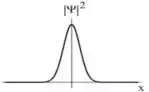
Em um instante inicial, podemos esperar que a função densidade de probabilidade seja do tipo:

Ψ x , 0 2 = 2 a π   e - 2 a x 2

Portanto, o gráfico para esse instante tem a forma:

Passo 3

Agora, com o passar do tempo, podemos perceber que, como ω é uma função decrescente de t , isto é, ela apenas diminui, a densidade de probabilidade

Ψ x , t 2 = 2 π     ω   e - 2 ω 2 x 2

Possui um pico mais atenuado e, além disso, está mais distribuída ao longo do eixo x , como indica o gráfico a seguir:

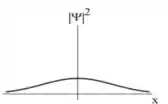
Perceba que isso significa que com o passar do tempo, a probabilidade de encontrar a partícula próxima à origem diminui, como era de se esperar!

Resposta

Ψ x , t 2 = 2 π     ω   e - 2 ω 2 x 2

Ver Outros Exercícios desse livro