Uma partícula move-se de modo que suas coordenadas, como funções do tempo, são dadas por x = v0t, y = y0 sen wt. (a) Faça os gráficos de x e y como funções de t. (b) Faça o gráfico da trajetória da partícula, (c) Que força é necessária para produzir esse movimento? (d) Calcule os módulos da velocidade e da aceleração como função do tempo.

Faaala, galera!!! Nós temos duas equações: uma linear, e outra senoidal, certo? Assim, teremos os gráficos com os seguintes padrões:

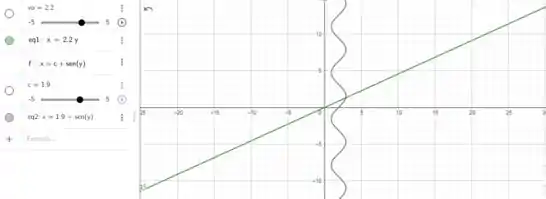
em que a linha verde é a equação de x e a linha cinza, a equação de y. Sendo assim, a força necessária para produzir este movimento seria a soma das forças dos movimentos em x e y:

Por fim, teremos que a velocidade e a aceleração em função do tempo serão:

v= vo+at²/2, com a=v/t.