Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
Uma partícula parte da origem em e se move no sentido positivo do eixo . O gráfico da velocidade da partícula em função do tempo é mostrado na Figura ; a escala vertical do gráfico é definida por .
Qual é a coordenada da partícula em ?
Qual é a velocidade da partícula em ?
Qual é a aceleração da partícula em ?
Qual é a velocidade média da partícula entre e ?
Qual é a aceleração média da partícula entre e ?
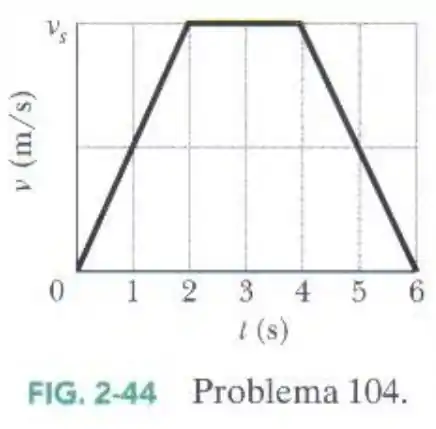
Passo 1
Sabendo que a posição pode ser encontrada pela área do gráfico da velocidade com o tempo então a posição em será a soma das áreas abaixo:
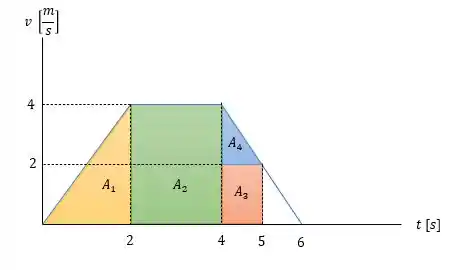
Onde já podemos notar que a velocidade em será de pois no gráfico dado no enunciado temos a velocidade em sendo a metade de (isso nos responde a letra se você olhar o enunciado), portanto a posição dessa partícula em será:
Ou seja a soma das áreas (triângulo amarelo), (retângulo verde), (retângulo laranja ) e (triângulo azul).
O que será:
Fazendo essa conta teremos:
Passo 2
A aceleração em pode ser vista como a variação da velocidade mas como ver isso, bem note que em a velocidade é uma reta decrescente, então o coeficiente angular dessa reta (que é a variação de qualquer reta) valerá:
Onde é a velocidade em e é a velocidade em , portanto:
Passo 3
Na letra queremos a velocidade média e para encontrar esse valor nós temos que fazer:
Onde temos a posição em no tempo 2 sendo a posição final diminuído da posição inicial dividido pelo intervalo de tempo. Isso independente da trajetória que o corpo faça.
Na letra temos pelo gráfico que a posição em será igual a área do triângulo amarelo abaixo:
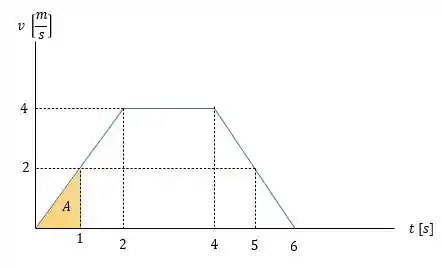
Então:
Portanto a velocidade média entre e será:
Passo 4
De forma parecida a aceleração média será calculada por:
E como a velocidade em é igual a velocidade em e vale então: