a) Uma partícula com velocidade inicial colide com um elétron livre em repouso. Mostre que, se supomos que a massa da partícula é de cerca de vezes a massa do elétron, a deflexão máxima da partícula é de aproximadamente .
b) Mostre que a deflexão máxima de uma partícula que interage com a carga positiva de um átomo de Thomson de raio é também de cerca de .
Passo 1
Fala galerinha, beleza?
Tem um erro no enunciado do livro: a massa da partícula alfa é vezes maior que a massa do elétron, não .
Vamos considerar primeiro a situação do item (a). Uma partícula de massa colide frontalmente com um elétron de massa inicialmente em repouso.
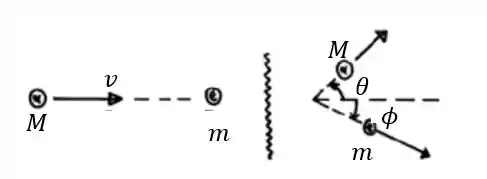
A partícula alfa é espalhada por um ângulo e o elétron por ângulo . Vamos considerar que o problema é não relativístico.
Assim, a conservação do momento da direção horizontal nos fornece
Estou chamando de a velocidade da partícula alfa após a colisão e a velocidade do elétron.
A conservação do momento na direção vertical dá
Observe que
Elevando as duas equações ao quadrado e somando:
Usando as relações trigonométricas, temos
Guarde essa equação!
Passo 2
Agora vamos olhar para a conservação da energia:
Ou ainda,
Podemos igualar com a equação do passo 1:
Agora o trabalho é isolar . Fazendo isso, encontramos:
Como queremos maximizar o ângulo, devemos ter
Assim,
Portanto,
Substituindo de volta, temos
Agora vamos usar uma aproximação importante:
Assim, temos
Além disso, para ângulos pequenos, temos
Portanto, obtemos
Como , temos
Passo 3
Agora vamos para o item (b).
Quando a partícula alfa interagir com o átomo de Thomson (uma esfera uniformemente carregada com carga e raio ), vai sofrer ação de uma força em um intervalo de tempo , de modo que a variação do momento na direção vertical vai ser
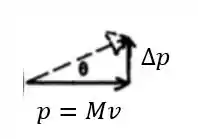
Supondo que o ângulo da deflexão é pequeno, podemos escrever
Podemos estimar o tempo de interação como sendo a o tempo necessário para percorrer uma distância (diâmetro do átomo) a uma velocidade :
Já a força, podemos considerar a lei de Coulomb:
Usando e , temos
Assim,
Portanto,
Identificando a energia cinética no denominador, temos
Usando , (para o ouro), e , obtemos
PS: a escolha é razoável para partículas alfas não relativísticas!
Resposta
Demonstração.