Se uma pedra é lançada verticalmente para cima com velocidade v, ela deve subir até uma altura h dada por v^2 = 2gh. Em particular, v² deve ser proporcional a h. Para verificar esta proporcionalidade, um estudante mede v e h por sete lançamentos diferentes e obtém os resultados apresentados na Tabela 2.11.

(a) Desenhe um gráfico de v por h, incluindo barras de erro verticais e horizontais. O seu gráfico é consistente com a predição de que v^2 « h?

(b) A inclinação da reta do seu gráfico deve ser 2g. Para determinar inclinação, desenhe o que parece ser a melhor reta passando pelos pontos e então meça a sua inclinação. Para determinar a incerteza na inclinação, desenhe as retas mais acima e mais abaixo que parecem se ajustar aos dados, razoavelmente. As inclinações destas retas fornecem o maior e o menor valor provável da inclinação. Seus resultados são consistentes com o valor aceito 2g = 19,6 m/s²?

Vamos realizar o gráfico no programa SciDavis, para que você possa entender melhor como ficaria o gráfico com estes dados. Plotamos o gráfico com os resultados obtidos na tabela do problema, teremos:

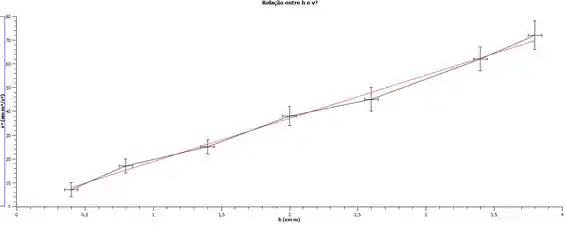
O aplicativo SciDavis apresenta um dado muito importante quando realizamos gráficos: o valor de R. Este R é um parâmetro que dita se o experimento foi realizado de forma precisa, ou seja, se as incertezas e os valores correspondentes estão próximos do esperado. Quanto mais próximo de 1, mais exato está o gráfico.

Aqui, neste caso, obtivemos um gráfico de R= 0.9989875. Isso nos mostra que sim, há a proporcionalidade esperada, já que além de tudo a reta vermelha está, em todos os casos, dentro dos valores da incerteza.

Além disso, no mesmo programa, conseguimos encontrar a inclinação da reta. Esta inclinação foi, neste caso, de 19,3, o que é, sim, próxima ao que se especulou no exercício, ou seja, a diferença deste valor até o ideal é de 0,3, menor que as incertezas dadas pelo problema. Logo, concluímos que os resultados são sim consistentes ao esperado!