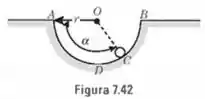
Uma pequena bola de massa , inicialmente em , desliza sobre uma superfície circular sem atrito (Fig. ). Demonstre que, quando a bola está no ponto , a velocidade angular e a força exercida pela superfície são , .

E aí, beleza?? Vamos primeiramente demonstrar que a velocidade da partícula em um ponto depende apenas da altura que ela caiu. Seja o ângulo que a velocidade da partícula faz com a horizontal em um dado instante, assim, temos:

Na última equação, foi utilizada a regra da cadeia, em que é um diferencial de caminho percorrido (inclinado). Assim, vem:

Note que . Assim, vem:

Sendo a altura que o corpo caiu.