Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 20.Problemas - Ex. 56

A potencia máxima que pode ser extraída de uma turnia de vento acionada por uma corrente de ar pode ser extraída de uma turbina de vento acionada por uma corrente de ar é aproximadamente

P = k d 2 v 3

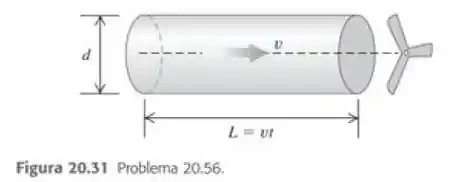
onde d é o diâmetro da lâmina, v é a velocidade do vento e k = 0,5   W ⋅ s 3 / m 5 .a) Explique a dependência de P em relação a d e v considerando um cilindro de ar passando sobre a lâmina da tubina no instante t (Figura 20.31). Esse cilindro possui diâmetro d , comprimento L = v t e densidade ρ .b) A turbina de vento Mod-5B em Kahaku, na ilha Oahu do Havaí, possui uma lamina com 97 m de diâmetro (comparável a um campo de futebol) e localiza-se no alto de uma torre de 58 m. Essa turbina pode produzir uma potencia elétrica de 3,2 MW. Supondo uma eficiência de 25 % , qual é a velocidade do vento necessária para produzir essa potencia? Dê a resposta em m/s e km/h. c) As turbinas de vento comerciais são localizadas geralmente nas passagens entre morros ou, de modo geral, na direção do vento. Por quê?

Passo 1

A potência máxima que pode ser extraída é a energia cinética total K da massa de ar que passa

sobre as pás da turbina no tempo t . Trabalho mecanico.

O volume de um cilindro de diâmetro d e comprimento L é π d 2 4 L .  

A energia cinética é 1 2 m v 2 .

Passo 2

  1. O cilindro descrito contém uma massa de ar

    2. m = ρ π d 2 4 L

    e assim a energia cinética total é

    K = ρ π 8 d 2 L v 2 .

    Essa massa de ar passará pela turbina em um tempo

    t = L v ,

    e assim a potência máxima é

    P = K t = ρ π 8 d 2 v 3 .

    Numericamente, o produto

    ρ a r = π 8 ≈ 0,5 k g m 3 = 0,5   W ⋅ s 3 m 5 .

    Isso completa a prova.

    Passo 3

  2. a velocidade do vento necessária para produzir essa potencia é:

    3. v = P / e k d 2 1 / 3 = 3,2 × 10 6   W 0,25 0,5   W ⋅ s 3 m 5 97 m 2 1 / 3 = 14 m s = 50 k m h .

    Passo 4

  3. As velocidades do vento tendem a ser mais altas nas passagens nas montanhas.

Resposta

  1. ρ a r = π 8 ≈ 0,5 k g m 3 = 0,5   W ⋅ s 3 m 5
  2. 50 k m h
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bomba térmica é usada para aquecer um edifício. A temperatura externa é - 5 ° C e a temperatura no interior do edifício deve ser mantida a 22 ° C . O coeficiente de desempenho da bomba é 3,8 e a b
O motor de um refrigerador tem uma potência de 200 W . Se o compartimento do congelador está a 270 K e o ar externo está a 300 K , e supondo que o refrigerador tem a mesma eficiência que um refrigerad
O motor elétrico de uma bomba térmica transfere energia na forma de calor do exterior, que está a - 5 ° C , para uma sala que está a 17 ° C . Se a bomba térmica fosse uma bomba térmica de Carnot (uma
Para fazer gelo, um refrigerador, que é o inverso de uma máquina de Carnot, extrai 42 k J na forma de calor a - 15 ° C durante cada ciclo, com um coeficiente de desempenho de 5,7 . A temperatura ambie
Um condicionador de ar operando entre 93 ° F e 70 ° F é especificado como tendo uma capacidade de refrigeração de 4000 B t u / h . O coeficiente de desempenho é 27 % do coeficiente de desempenho de um