Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 20.Problemas - Ex. 53

Um Passat tem um motor a gasolina com seis cilindros operando com o ciclo Otto a uma razão de compressão r=10,6. O diâmetro do cilindro, chamado de furo do motor, é igual a 82,5 mm. A distancia que o pistão percorre durante a compressão mostrada na Figura 20.5, chama de curso, é 86,4 mm. A pressão inicial da mistura de ar com gasolina (no ponto a da Figura 20.6) é 8,50 × 10 4   P a , e a temperatura inicial é 300 K (igual à temperatura do ar externo). Suponha que 200 J de calor sejam fornecidos a cada cilindro em cada ciclo de queima de gasolina e que o gás possua C V = 20,5   J / m o l ⋅ K e γ = 1,40 . a) Calcule o trabalho total realizado em um ciclo em cada cilindro do motor e o calor rejeitado quando o gás se esfria até a temperatura do ar externo.b) Calcule o volume da mistura de ar com gasolina no ponto a   do ciclo.c) Calcule a pressão, o volume e a temperatura do gás nos pontos b ,   c e d do ciclo. Em um diagrama P V , mostre os valores numéricos de P ,   V e T em cada um dos quatros estados. d) Compare a eficiência desse motor com a eficiência de um ciclo de Carnot operando entre as mesmas temperaturas extremas.

Passo 1

Calcule e   da equação

e = 1 - 1 r γ - 1

Q C da equação

e = 1 - Q C Q H

e depois W da equação

W = Q = Q H + Q C = Q H - Q C .

Passo 2

  1. Assim,

    2. e = 1 - 1 r γ - 1 = 1 - 1 10,6 0,4 = 0,6111

    E

    e = Q H + Q C Q H

    e nos é dado Q H = 200   J ;

    Vamos calcular Q C :

    Q C = e - 1 Q H = 0,6111 - 1 200 J = - 78   J  

    (negativo, pois corresponde à saída de calor)

    Então,

    W = Q C + Q H = - 78   J + 200 J = 122   J .

    (Positivo, de acordo com a Figura 20.6.)

    Q H ,   W > 0 , e Q C < 0 para um ciclo do motor.

    Passo 3

  2. O tempo de estocagem do furo é igual à mudança de volume. O volume inicial é o final

    3. volume V vezes a taxa de compressão r . A combinação dessas duas expressões fornece uma equação para V . Para cada cilindro da área A = π   d / 2 2 , o pistão se move 0,864   m e o volume muda de r V para V , conforme mostrado a seguir:

    l 1 A = r V

    l 2 A = V

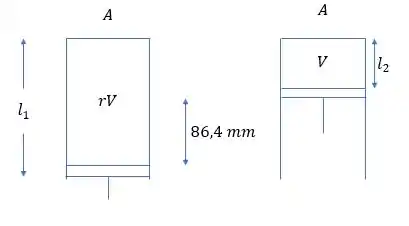
    E

    l 1 - l 2 = 86,4 × 10 - 3   m

    Assim,

    l 1 A - l 2 A = r V - V e l 1 - l 2 A = r - 1 V

    ⇒ V = l 1 - l 2 A r - 1 = 86,4 × 10 - 3   m π 41,25 × 10 - 3   m 2 10,6 - 1 = 4,811 × 10 - 5 m 3

    No ponto a o volume é r V = 10,6 4,811 × 10 - 5   m 3 = 5,10 × 10 - 4   m 3 .

    Passo 4

  3. Os processos no ciclo Otto são de volume constante ou adiabáticos. Usaremos Q H

    4. que é dado para calcular Δ T para o processo b c .

    Usaremos a equação T 1 V 1 γ - 1 = T 2 V 2 γ - 1 e p V   =   n R T para relacionar p , V e T para o parâmetro do processo adiabático a b e c d .

    p o n t o   a :

    T a = 300   K , p a = 8,50 × 10 4   P a , e V a = 5,10 × 10 - 4   m 3

    Passo 5

    p o n t o   b :

    V b = V a r = 4,81 × 10 - 5   m 3 .

    Processo a → b é adiabático, então T a V a γ - 1 = T b V b γ - 1 .

    T a r V γ - 1 = T b V γ - 1  

    ⇒ T b = T a r γ - 1 = 300   K 10,6 0,4 = 771   K

    p V = n R T então p V T = n R = c o n s t a n t e , então p a V a T a = p b V b T b .

    ⇒ p b = p a V a V b T b T a = 8,50 × 10 4   P a r V V 771 K 300 K = 2,31 × 10 6 P a

    Passo 6

    p o n t o   c :

    Processo b → c é de volume constante, então V c = V b = 4,8   1 × 10 - 5   m 3

    Q H = n C V ∆ T = n C V T c - T b .

    O problema especifica Q H = 200   J ; usaremos para calcular T c . Usaremos primeiro os valores de p, V, T no ponto a para calcular o número de mols n .

    n = p V R T = ( 8 , 50 × 10 4   P a ) ( 5,10 × 10 - 4   m 3 ) 8,31545 J m o l ⋅ K ( 300   K ) = 0,01738   m o l  

    Então

    T c - T b = Q H n C V = 200   J 0,01738   m o l 20,5 J m o l ⋅ K = 561,3   K

    E

    T c = T b + 561,3   K = 771   K + 561   K = 1331   K

    p T = n R V = c o n s t a n t e   então p b T b = p c / T c

    ⇒ p c = p b T c T b = 2,32 × 10 6   P a 1331   K 771   K = 4,01 × 10 6   P a  

    Passo 7

    p o n t o   d :

    V d = V a = 5,10 × 10 - 4   m 3

    Processo c → d é adiabático, então T d V d γ - 1 = T c V c γ - 1

    T d r V γ - 1 = T c V γ - 1

    ⇒ T d = T c r γ - 1 = 1332 K 10,6 0,4 = 518   K  

    p c V c T c = p d V d T d

    ⇒ p d = p c V c V d T d T c = 4,01 × 10 - 6   P a V r V 518 K 1332 K = 1,47 × 10 5   P a

    Passo 8

  4. A eficiência de Carnot é dada pela equação:

e C A r n o t = 1 - T C T H = T H - T C T H .

T H é a temperatura mais alta atingida no ciclo e T C é o mais baixo.

Na parte (a), a eficiência desse ciclo Otto é e = 0,611 = 61,1 % .

A eficiência de um ciclo de Carnot operando entre 1332 K e 300 K é

e C a r n o t = 1 - T C T H = 1 - 300 K 1332 K = 0,775 = 77,5 % ,

qual é maior.

A 2ª lei exige que e   ≤   e   ( C a r n o t ) , e nosso resultado obedece a essa lei.

Resposta

  1. W = 122   J
  2. 5,10 × 10 - 4   m 3
  3. p o n t o   a : T a = 300   K , p a = 8,50 × 10 4   P a , e V a = 5,10 × 10 - 4   m 3

    4. p o n t o   b : T b = 771   K , p b = 2,31 × 10 6 P a , e V b = 4,81 × 10 - 5   m 3

    p o n t o   c : T c = 561,3   K , p c = 4,01 × 10 6   P a   , V c = 4,8   1 × 10 - 5   m 3

    p o n t o   d : T d = 518   K , p d = 1,47 × 10 5   P a , V d = 5,10 × 10 - 4   m 3

  4. e C a r n o t = 77,5 %   maior.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

“Até onde sabemos, a Natureza nunca desenvolveu uma máquina térmica” – Steven Vogel, Dispositivos da Vida. (a) Calcule o rendimento de uma maquina térmica operando entre a temperatura do corpo ( 98,6
Recentemente, um antigo projeto de máquina térmica, conhecida como a máquina de Stirling, foi anunciado como uma maneira de se produzir potencia a partir da energia solar. O ciclo de uma máquina de St
Uma máquina, usando 1,00m o l de um gás ideal, inicialmente em um volume de 24,6 L e a uma temperatura de 400 K , realiza um ciclo que consiste em quatro etapas: (1) uma expansão isotérmica à temperat
Um gás diatômico ideal segue o ciclo mostrado na figura 19-16. A temperatura do estado 1 é 200 K . Determine (a) as temperaturas dos outros três estados numerados do ciclo e (b) o rendimento do ciclo.
A figura 19-15 mostra o ciclo seguido por 1,00m o l de um gás monoatômico ideal com um volume inicial V 1 = 25,0 L . Todos os processos são quase-estáticos. Determine (a) a temperatura de cada estado