O processo abc mostrado no diagrama PV da Figura E19.11 envolve 0,0175 mol de um gás ideal. (a) Qual foi a temperatura mais baixa que o gás alcançou nesse processo? Onde ele ocorreu? (b) Quanto trabalho foi realizado pelo gás ou sobre o gás de a para b? E de b para e? (c) Se 215 J de calor fossem colocados no gás durante abc, quantos desses joules entraram na energia interna?
Passo 1
Faaaaala meu povo, bora pra mais uma questão do nosso livro!
Para essa questão, primeiramente tratamos de um gás ideal com número de mols igual a .
E temos o seguinte diagrama:
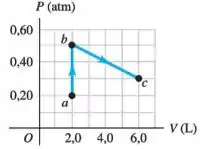
Com esses dados a gente pode segui na nossa resolução.
Passo 2
Letra a)
Conforme mostrado na figura o processo é o primeiro processo onde a pressão aumenta, enquanto o volume é constante e a temperatura mais baixa é a inicial que pode ser determinada na figura no ponto . Onde no ponto a pressão e o volume . Agora podemos aplicar a lei do gás ideal para determinar a temperatura mais baixa e apontar .
Onde é o número de mols e é a constante do gás e é igual a . Agora substitua por todos os nossos valores na equação do gás ideal para calcular a temperatura . Mas primeiro, converta as unidades de de atm para multiplicando seu valor () e de multiplicando seu valor por .
Passo 3
Letra b)
No processo , o volume do gás é constante, portanto, não há expansão ou compressão aplicada ao gás, portanto não há trabalho realizado e é igual a zero.
No processo , a pressão diminui de para , mas o volume aumenta de para . Portanto, o trabalho realizado é igual à área sob a curva onde está a primeira dimensão e a segunda dimensão é . Faça a contagem, o processo é meio de um processo cíclico, então o trabalho realizado será igual à metade da área e seria dado por:
Passo 4
Letra c)
Sabendo que:
Para encontrar o trabalho realizado, usamos a equação abaixo:
Substituindo temos:
Chegamos ao fim de mais uma questãozinha!
Tudo certo? Te vejo na próximaaaaa!
Resposta
Letra a)
Letra b)
Letra c)