Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Mecânica- Ed: 2º - Capítulo 4.Problemas - Ex. 51

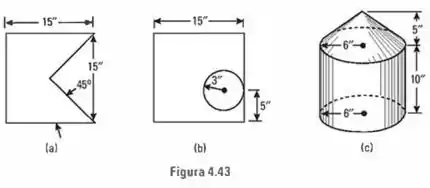
Procure o centro de massa dos três corpos homogêneos mostrados na Fig. 4.43.

Passo 1

E aí, beleza?? Para resolver os três itens usaremos o princípio da superposição. Para o item (a), temos, ao assumir que o ponto 0,0 se encontra no vértice inferior esquerdo do quadrado e que o quadrado possui densidade σ e que o buraco triangular possui área A :

σ ∙ 3 A ∙ x c m = σ ∙ 4 A 15 2 - σ ∙ A ∙ 15 2 + 2 3 ∙ 15 2

3 x c m = 30 - 25 2 = 35 2

Logo:

x c m = 35 6

Para o eixo y :

σ ∙ 3 A ∙ y c m = σ ∙ 4 A 15 2 - σ ∙ A ∙ 15 2 = 3 σ A ∙ 15 2

Logo:

y c m = 15 2

Assim:

C M = 35 6 , 15 2

Passo 2

Agora para o item (b), os centros de massa do quadrado e do círculo são:

C M q = 15 2 , 15 2

C M c = 12,2

Assim, temos:

15 2 - 9 π x c m = 15 2 ∙ 15 2 - 9 π ∙ 12 ∴ x c m = 6,85 ' '

15 2 - 9 π y c m = 15 2 ∙ 15 2 - 9 π ∙ 2 ∴ y c m = 8,3 ' '

Passo 3

Por fim, no item (c), devido à simetria, temos que o C M está sobre o eixo que passa pelo centro do cilindro e do cone. Sendo ρ a densidade do material, a sua altura é dada por:

ρ π ∙ 6 2 ∙ 10 + 1 3 π ∙ 6 2 ∙ 5 y c m = 5 ∙ ρ ∙ π ∙ 6 2 ∙ 10 + 12,5 ∙ ρ ∙ 1 3 π ∙ 6 2 ∙ 5  

Portanto:

y c m = 6,07 ' '

Resposta

(a)

C M = 35 6 , 15 2

(b)

C M = 6 . 85   ,       8.3

(c)

0 ,   6.07,0

Ver Outros Exercícios desse livro