Prove que o campo gravitacional e o potencial de um filamento fino, que tem uma massa . por unidade de comprimento, são dados por:
E , respectivamente, onde é a distância do ponto ao filamento. (Sugestão: determine, inicialmente, em vista ela simetria, qual é a direção do campo e as variáveis que o determinam. Em seguida, divida o fio em pequenos segmentos, cada um com um comprimento , de calcule a componente do campo devido a esse segmento, na direção do campo resultante. Uma vez obtido, por integração, o campo resultante, pode-se obter o potencial gravitacional a partir do campo, utilizando a Eq. (13.21).]
Passo 1
E aí, beleza?? Vamos utilizar para resolver esse problema a Lei de Gauss da gravitação, em vez da sugestão dada no problema, devida à simetria da situação, que implica em um campo gravitacional na direção radial, para dentro. Considere a seguinte Gaussiana:
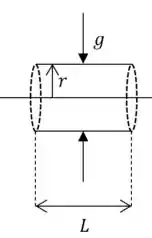
Assim, da Lei de Gauss, temos:
Portanto:
Como esse campo aponta para dentro, vem:
Passo 2
Dessa maneira, o potencial fica:
Que, a par de uma constante, temos:
Resposta
Ei, a resposta está no passo a passo :)