Prove que (onde , e são vetores e é um escalar variável) representa uma parábola situada no plano determinado pelos vetores e e que passa pelo ponto cujo vetor de posição é .
Passo 1
E aí, beleza?? Primeiramente, perceba que o vetor determina apenas a origem do sistema de coordenadas. Dessa maneira, a curva possui o mesmo formato de , sendo apenas deslocada. Portanto, vamos trabalhar com por simplicidade. Considere então o seguinte sistema de coordenadas, sendo o eixo orientado paralelamente ao vetor :
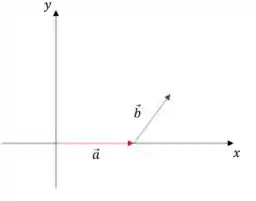
Assim, sendo , vem:
Passo 2
Desse modo, isolando :
Ou seja:
Ou ainda:
Que é a equação de uma parábola. Portanto, o lugar geométrico dos pontos definidos por e, portanto, por , é uma parábola, como queríamos demonstrar.
Resposta
Ei, a resposta está no passo a passo :)