Usando métodos vetoriais, determine: (a) o comprimento das diagonais de um cubo; (b)o ângulo das diagonais com os lados adjacentes; (c) o ângulo das diagonais com as faces adjacentes; (d) o ângulo entre as diagonais.
Passo 1
E aí, beleza?? Considere o seguinte cubo para resolução da questão:
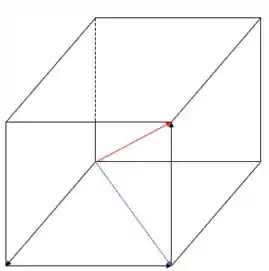
Para o item (a), podemos determinar o valor das diagonais azul () e vermelha () da seguinte maneira:
Portanto:
Passo 2
Agora, para o item (b), basta tomarmos o produto escalar com os vetores unitário em cada direção. No caso da diagonal , ela faz um ângulo de com um dos lados e com os outros dois faz um ângulo igual a:
Agora o faz com os lados adjacentes um ângulo dado por:
Passo 3
Para o item (c), teremos os mesmos ângulos obtidos no item anterior, pois os vetores que definem as superfícies também estão orientados ao longo dos eixos. Assim, faz com o vetor normal a uma das faces (pertence a essa face) e faz um ângulo com as outras duas. Da mesma maneira, a diagonal faz um ângulo com as três faces adjacentes.
Passo 4
Para o item , basta tomarmos o produto escalar das diagonais:
Logo:
Resposta
(a)
(b)
(c) faz com o vetor normal a uma das faces (pertence a essa face) e faz um ângulo com as outras duas. Da mesma maneira, a diagonal faz um ângulo com as três faces adjacentes.
(d)